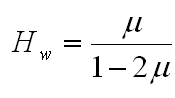
An ANSI-C compliant program has been developed to explore the performance of BBC-based concurrent codes in a data visualistic way.
The core of the program is a Concurrent Codec that generates a transmission packet formatted as a monochrome bitmap image. Each bit in the image represents a bit in the packet, beginning at the upper left corner and proceeding to the lower right corner in a row-wise fashion.
It's one thing to be able to extinguish most, if not all, of the hallucinations at the end, but if the number of potential messages that must be tracked grows beyond acceptable limits then the communications channel still becomes jammed. Thus a more relevant metric of codec performance is the number of working hallucinations that exist throughout the process path. A working hallucination is a partial message that exists at some point in the decoding process but does not lead to one of the true messages in the end. The hallucination workload density, Hw, is simply the number of working hallucinations divided by the number of actual messages.
A direct measure of the impact of working hallucinations is the number of calls to the hash function used in the decoding process. This is because, at each stage in the decoding process, a partial message, be it real, rogue, or hallucination, results in two calls to the computationally expensive hash function - one to see where the next mark will be if the message continues with a 0 as the next bit and one to see where a mark will be if it continues with a 1. For a single message in a packet in a noise-free environment, each bit in the message will normally result in two calls to the hash function. Occasionally, both potential follow-on bits will be present resulting in the next stage of decoding making a total of four calls to the hash function. However, not only is this a rare event, but the likelihood that many of the successive hallucinations will survive another stage becomes vanishingly small for a very sparse packet.
Note that this is not the case for a packet that is not very sparse. In fact, if u is the packet mark density, then at any given state each actual message will produce, on average, u hallucinations in the next stage (in addition to the message itself) while each working hallucination will produce 2u . After several stages (tens, not thousands) the number of working hallucinations co-existing with each legitimate message in steady state is
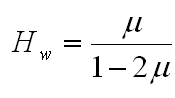
Although the above relationship can be easily arrived at by modeling the number of hallucinations at each stage statistically, it can be derived even quicker by a simple model of the steady-state behavior. If the number of hallucinations per actual message at stage N is Hw, then the total number of partial messages per actual message at this stage is simply (Hw+1). The number of messages carried to the next stage will, on average, consist of the actual message, the u hallucinations due to it, and the 2u hallucinations for each of the Hw hallucinations in the current stage. Thus the number of hallucinations at state N+1 is u(1+2Hw). In steady state, this will still be equal to Hw and solving for Hw yields the above relationship.
Notice that at a mark density of 1/3, there will be, on average, one hallucination for each real message. Since both the real message and the hallucination will require two calls to the hash function to determine which partial messages are carried into the next stage, a mark density of 1/3 would be expected to result in a steady state performance of four hash function calls per message at each stage of processing.
It is a simple matter to track the number of hash function calls made at each stage of processing but the number of hallucinations can't, in general, be known until after processing is complete. However, given the number of hash function calls at a given stage it is a simple matter to back out the number of working hallucinations by recognizing that there are two calls per partial message and one of those messages is not an hallucination. Hence divide the hash function call density by two and subtract one.
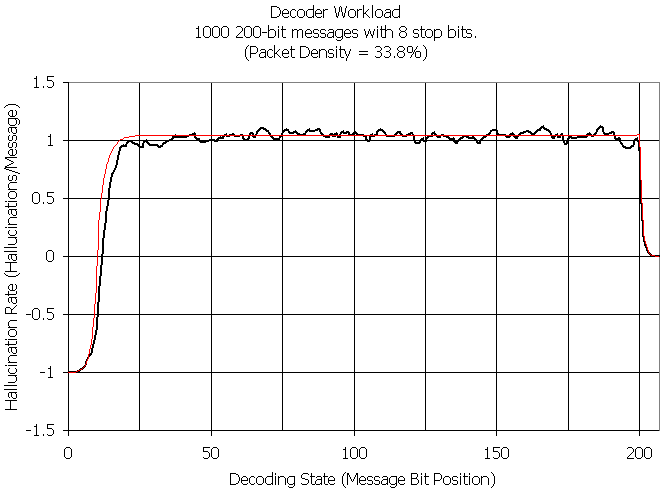
The following graph shows the experimental results (thick line) for a message packet containing 1000 messages resulting in a mark density of 33.8%. As can be seen, the actual performance almost perfectly matches the predicted (thin red line) 4.09 hash calls per message (the asymptotic value given by the above equation is 4.17).
The initial hallucination rate is negative because of an artifact of the definition of the hallucination rate being the fractional increase in working messages relative to the number of actual messages. Initially the number of working messages, real or otherwise, is limited at stage N by the 2N possible bit sequences at that stage. Thus for packets containing more than a single message there are initially fewer partial messages than there are actual messages resulting in an apparent negative number of hallucinations. For instance, a packet containing a 1000 messages can't even reach 1000 partial messages until the 10th stage. However, as the data shows, once that limiting number of stages is reached, the actual number of working messages quickly approaches the steady state level predicted by the theory.
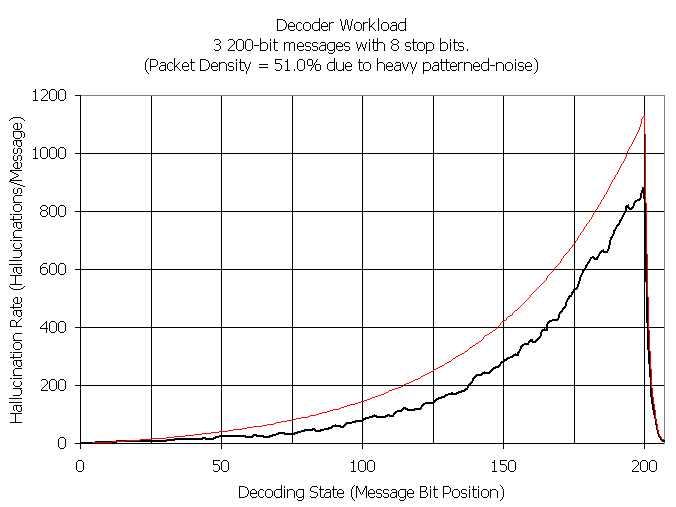
Once the stop bits come into play, the number of surviving hallucinations drops exponentially.
As the packet mark density grows above 1/3, the workload begins to rise exponentially with message length. However, even for densities in the 50% range (the point at which theory predicts the steady state number of working hallucinations will become infinite) the growth rate is tame enough to permit continued decoding as demonstrated by the following results. Notice that the ability of the stop bits to extinguish the hallucinations that survive the message-body decoding is still clearly evident. The deviation between the experimental and theoretical results is not surprising since exponential functions propagate even minor deviations exponentially.