(Last Mod: 27 November 2010 21:56:33 )
This page is devoted to providing an introduction to working with finite fields of the type used in cryptography. While the goal is to provide enough depth so that the reader can gain a decent feel for the underpinnings of the material, no real attempt is made to be absolutely rigorous or complete in the construction and description of the concepts presented here. Instead the focus is to foster a more intuitive feeling for the material based primarily on establishing that the various concepts and choices made are reasonable and well-grounded. As a result, it is believed that the reader will discover that the material is developed in such a way that a much better understanding of the concepts is possible than is likely to be gained with many of the cryptography books on the market which tend to either present a bunch of algorithms in cookbook fashion or present the number theory topics at a level of depth that requires a stronger abstract algebra background than most readers possess.
Recall from the discussion of finite fields, that a finite field is an algebra consisting of a set of elements and two operators that act on those elements. We are free to define the elements and the operators in any way we choose provided the properties required of a finite field are satisfied. Those requirements are:
Further recall that to be an abelian group, the following properties must hold with respect to the operator:
If n=1, then we have the finite field GF(p) where p is a prime number. The specific finite fields of this form that we have been working with are merely our old friends the "mod-p" worlds where our first operator is everyday normal addition except that the result is always reduced modulo-p and where our second operator is everyday normal multiplication except that the result is, once again, always reduced module-p. Before you proceed any further, be sure that you understand the following things:
The key to the second point is that if n is not prime, then there will exist some elements within the residue set (namely those that are not relatively prime to n) for which no multiplicative inverse exists.
At the risk of belaboring a point, keep in mind that GF(p) and a "mod-p world" are not the same. We are free to construct the elements and functions in GF(p) however we like provided the requirements for a finite field are met. A "mod-p world" is simply one example of a construction of a GF(p) finite field. Having said that, in the remainder of this document, references to GF(p) can be taken to mean "mod-p" unless stated otherwise without loss of generality.
Before proceeding, it is important to understand that we can't simply use a "mod-pn world" to construct a GF(pn) finite field if n is greater than one. The reason should be obvious; pn is not a prime number under these conditions and therefore there will be elements that lack multiplicative inverses. So we can't just use a set of integers and use normal addition and multiplication, even reduced modulo-pn.
Once again, we are free to choose our elements and define our operators in any way that works, but it only makes sense to start with something with which we are already familiar and which almost works and then make as few modifications as necessary to get it to work. It turns out that one way (not the only way) to do this is to define our set of symbols to be a set of polynomials. Then we can use normal polynomial arithmetic (addition and multiplication) as the starting point for our two operators since they already satisfy most of the properties we need.
So let's get started. The finite field GF(pn) requires pn elements and two operators that act on those elements, so the first step is to define the set of elements.
As a first step, let's devise a set of symbols that let's us easily represent pn things. The obvious answer is to represent them as an n-digit "number" in base-p. What we need to keep in mind, however, is that these are not numbers, they are just pn symbols that, at this point, have absolutely no order and no relation to each other - we could just as easily and validly used {Fred, Bob, Sue, Jane, ..., Dick, Harry} as our set of symbols. There is a very strong tendency to subconsciously perceive something that looks like a number as a number and treat is as a number even when it isn't. This can cause problems if we aren't on guard for it, which is why it is mentioned repeatedly in this discussion.
Having said that, let's for a moment treat our symbols as numbers and use that to make the step from representing numbers to representing polynomials a bit easier to see. For this example, let's use the symbols from GF(75). The symbols in such a field would (okay, could) look just like a 5-digit base-7 number such as 36524. We can write this number as follows:
36524 = (3)(74) + (6)(73) + (5)(72) + (2)(71) + (4)(70)
If we replace the number base with the variable D we have the following polynomial expression:
36524 = 3D4 + 6D3 + 5D2 + 2D1 + 4D0
We know that polynomials obey the normal rules of addition and multiplication, so let's see if we can leverage that.
It is very tempting to think that, in this case, D is equal to 7. That is not the case. We have now made the transition from 36524 being a base-7 integer to 36524 being nothing more than a symbol in an arithmetic system that represents a polynomial in the variable D. Even after accepting that, there is a natural tendency to want to solve for D or think that the value of D has some meaning since that is what we are used to when working with most polynomial expressions. But that simply isn't the case here; D is just a dummy variable used to construct a polynomial expression and that polynomial expression itself is an element in the finite field we are constructing. Our operators will act on this, and other, polynomials and the results of those operations will be polynomials that are also in the set of elements for this finite field.
Keep in mind that the reason we are using polynomials is for convenience; it simply makes it easier to define how our two operators map combinations of symbols to other symbols. For instance, our familiar rules make it easy for us to remember that (D+2) + (3D+1) maps to (4D+3). We could just have easily have defined addition such that (Bob) + (Sue) maps to (Harry), but that would be very hard for us to use and get comfortable with. Both are equally valid, just not equally as handy. Be careful not to put more meaning into these polynomials than is there.
At this point what we have accomplished (an all the we have accomplished) is a systematic way of representing pn symbols as unique polynomial expressions. We still have to define two operators, which we will call additional and multiplication, such that all of the required properties of an algebraic field are satisfied. Let's first deal with addition and see how we can define it to obtain an abelian group. Once we have this we can examine multiplication and see how we can define it to be an abelian group on the set consisting of all of our polynomials except the additive identity polynomial. Finally, we just need to ensure that multiplication is distributive over addition.
As stated above, we need to define our addition operator such that when it acts on the set of polynomials we've defined for GF(pn) that we have an abelian group, namely one that is closed, commutative, associative, has an identity element, and contains an additive inverse for each element in the set. We know that normal polynomial addition is commutative and associative, so we just need to avoid doing anything that would invalidate these properties. Likewise, we know that polynomial addition has an identity element, namely 0, and that this element is a member of our set. Thus three of our five properties are satisfied without any modification of the addition rules for everyday polynomials.
However, the remaining two properties, closure and additive inverse, are not satisfied by normal polynomial addition. For example, let's consider adding the two polynomials 36524 and 50452 from the GF(75) world we started constructing previously. Using normal polynomial addition, this gives us:
36524 = 3D4 + 6D3 + 5D2 + 2D1 + 4D0
+ 50452 = 5D4 + 0D3 + 4D2 + 5D1 + 2D0
-----------------------------------------------
?6??6 = 8D4 + 6D3 + 9D2 + 7D1 + 6D0
As you can see, there are at least some elements of the set that we cannot add together and represent using one of the defined polynomials in our set. Similarly, the additive inverses are not present in the set:
36524 = 3D4 + 6D3 + 5D2 + 2D1 + 4D0
+ ????? = -3D4 + -6D3 + -5D2 + -2D1 + -4D0
-----------------------------------------------
00000 = 0D4 + 0D3 + 0D2 + 0D1 + 0D0
However, neither of these should cause too much concern because these two properties weren't initially satisfied for working in a mod-p world either until we made a minor tweak to the definition of addition - namely the concept of reducing the result modulo-p. If we add two polynomials of degree d then we get a polynomial of, at most, degree d. Since all of the symbols in our set are polynomials of degree (p-1) or less, this means that we have a good start at obtaining closure under addition since it's only the coefficients that are an issue. So what if we perform the addition of the coefficients in GF(p)?
In making this minor modification to the normal polynomial addition operation we have obtained closure. For example:
36524 = 3D4 + 6D3 + 5D2 + 2D1 + 4D0
+ 50452 = 5D4 + 0D3 + 4D2 + 5D1 + 2D0
-----------------------------------------------
16206 = 1D4 + 6D3 + 2D2 + 0D1 + 6D0
We have also obtained a complete set of inverse elements. For example:
36524 = 3D4 + 6D3 + 5D2 + 2D1 + 4D0
+ 41253 = 4D4 + 1D3 + 2D2 + 5D1 + 3D0
-----------------------------------------------
00000 = 0D4 + 0D3 + 0D2 + 0D1 + 0D0
Note how, in neither case, could we have simply treated the five digit symbols as integers and added them together to get the correct result, once again emphasizing the point that even though they may look like numbers, they are not numbers and can't be treated as such.
Finally, we have done this without upsetting any of the other three properties that were already satisfied.
To summarize, addition in GF(pn) is defined to be the normal polynomial addition except that the coefficients of each term are added in GF(p). Another way of saying this is that normal polynomial addition is used except that the coefficients are reduced modulo-p.
As with the addition operator, we want to leverage normal polynomial multiplication as much as possible. We once again get three of the five properties right away since normal polynomial multiplication is both commutative and associative and the normal multiplicative identity element, namely 1, is included in the set. So once again we just need to tweak our definition of multiplication so as to obtain closure and to ensure that each element (with the exception of the additive identity element, namely 0) has a multiplicative inverse polynomial that is in the set.
Using the same two polynomials from our GF(75) example above, the normal polynomial product of 36524 and 50452 would be:
36524 = 3D4 + 6D3 + 5D2 + 2D1 + 4D0
* 50452 = 5D4 + 0D3 + 4D2 + 5D1 + 2D0
-----------------------------------------------
????? = 15D8 + 30D7 + 27D6 + 49D5 + 76D4 + 45D3 + 36D2 + 24D1 + 8D0
However, we already know that one modification we need to make to our multiplication operator is to require that the polynomial coefficients be operated on in GF(p) in order to be consistent with how addition is performed on the coefficients. Without this, life would become very messy very fast and, almost certainly, we would not be able to satisfy the distributive property if nothing else. Even if this weren't the case, we would need to do so for the same reason as before - so that the coefficients always map back to those allowed by the set of polynomial symbols that has been defined. Doing this reduction on the previous result yields the following polynomial product:
????? = 1D8 + 2D7 + 6D6 + 0D5 + 6D4 + 3D3 + 1D2 + 3D1 + 1D0
We now need to map this back to our defined set of symbols by reducing it, somehow, to a polynomial of degree four or less. We will use the same basic concept, that of working in a modular world, to perform this reduction but we will need to work at the level of the polynomial as a whole and not at the level of the individual coefficients. There are two reasons for this. First, we have already imposed modular behavior on the individual coefficients and so we can't play that card a second time. Second, even if we could, it wouldn't change the fact that multiplication of two polynomials can result in a polynomial that is of a degree greater than allowed by our symbol set definition.
The first thought that probably comes to mind is to use a parallel of the modulus that is used in a normal mod-p world. If the result from a multiplication operation results in a polynomial of degree n or higher then we can divide it by a "modulus polynomial" and define the remainder polynomial to be the result of our multiplication operation.
Setting aside the fact that the polynomials are not intrinsically ordered, the obvious candidate for such a modulus polynomial would be D n since, in some very weak sense, it is "one greater" than the largest symbol in our set. At this point you should be thinking something along the lines that it only appears to be "one greater" when we view our symbols as integers and therefore this claim should be highly suspect right from the beginning since we know bad things generally happen when we let ourselves fall into that trap. We will have the same problem here, but let's pursue this path and see what lessons we learn.
If we divide the above polynomial by D5, we get a remainder of
63131 = 6D4 + 3D3 + 1D2 + 3D1 + 1D0
Life appears to be good and this is clearly a simple modulus to use, but does it really satisfy our needs as we try to construct a finite field?
As we found with a normal mod-p world, the modulus must be relatively prime to all the members in the set since those that aren't will not have a multiplicative inverse. If we use D5 as our modulus, we can clearly see that it is not relatively prime to all of the elements of the symbols set. For example:
D5 = D4 * D1
As a result, we might reasonably suspect that neither D1 nor D4 would have a multiplicative inverse, and our suspicion would be correct. The reasoning is directly analogous to the situation in a normal mod-p world.
Hence we need to choose a "primitive polynomial." But what is a primitive polynomial? We can't really use the name "primitive polynomial" to tell us much since we coined the name and could have called it anything. Instead, we need to define a primitive polynomial in terms of the properties we need it to possess.
Since we want a primitive polynomial to be suitable for use as a modulus, let's once again examine what properties we need the modulus in a mod-p world to possess. There are two obvious properties at this point: (1) the modulus must be relatively prime to all elements of the set and (2) whenever any possible element not in the set is divided by the modulus the result must be a remainder that is in the set. The first property requires that the modulus polynomial be "irreducible" meaning only that it is not divisible by any polynomial in the set. The second property requires that the polynomial be of no more than degree n since any higher degree could result in remainder polynomials that are of degree n or higher thus violating our requirements.
A third not-so-obvious property is that it must be possible to actually obtain all of the possible polynomials in the set as remainder polynomials. If this isn't the case, then we will almost certainly lose associativity and will almost certainly not be able to satisfy the distributability requirement. Don't be too concerned if the reason for this isn't obvious - it was stated as being a not-so-obvious property for a reason. Accepting that this is the case, however, the implication is that the modulus polynomial must be of no less than degree n since any lower degree will result in subsets of the set of polynomials that can't be produced by taking the remainder after dividing by the modulus polynomial. So we thus have the tighter requirement that our modulus polynomial must be an irreducible polynomial of degree n.
There is a fourth, even more subtle, property that a primitive polynomial must possess; namely it must be a "generator polynomial" for the entire set of polynomials. This means that, if M is the modulus polynomial, that (Dk mod M) must produce all polynomials in the set, except for the additive identity element, 0, as k varies from 0 to (pn-2). The reason for this requirement is subtle and will not be explained in any depth here. The basic issue is that if the modulus polynomial is not a generator of the entire set, then the multiplicative group, even if it is abelian, will not be cyclic and it turns out that only a cyclic multiplicative abelian group will satisfy the distributivity property that we need to complete our finite field. Do not be concerned if this makes little sense (meaning that this document needs to be expanded in the future in an effort to make it make sense, or at least seem like a reasonable requirement). For now take this one on faith.
To summarize, multiplication in GF(pn) is defined to be the normal polynomial multiplication except that the coefficients of each term are multiplied in GF(p) and the polynomial is reduced modulo a primitive polynomial. Another way of saying this is that normal polynomial multiplication is used except that the coefficients are reduced modulo-p and the final result is the remainder after normal polynomial division by a primitive polynomial.
There is no efficient algorithmic approach to finding primitive polynomials in GF(pn). For the special case of p=2, there are methods for constructing and/or testing primitive polynomials in GF(2n), but not for finding all of them in an efficient manner. This section will not make any attempt to delve into the efficient construction of primitive polynomials. Instead it will assume that a brute force search over all of the possibilities is required. In practice, tables of primitive polynomials can be referenced (though finding them for anything other than GF(2n) is difficult), software designed specifically to find primitive polynomials can be used, or you can delve deeper into the theory to learn how to do it yourself.
In a brute force search, a reasonable first step is to identify all of the irreducible polynomials of degree n. The second step is then determining which of those are primitive.
Two methods of identifying the irreducible polynomials come to mind. The first is to work through each possible irreducible polynomial of degree n and attempt to divide it by every possible polynomial of degree less than n. The second is to proceed in the opposite direction by producing polynomials of degree n by multiplying polynomials of degree less than n and eliminating the results from the list of possible irreducible polynomials. In the first approach, if done blindly, there are p(n+1) candidate polynomials and pn polynomials that need to be checked to see if they divide each candidate. Hence the order of complexity of identifying the irreducible polynomials using this method blindly is O(p(2n+1)). The second approach, if done blindly, requires each of the pn polynomials in the set to be multiplied pair-wise, including with themselves, resulting in a complexity of O(p2n). Although the second method only appears better than the first by a factor of p, there is also the fact that the first method involves polynomial division while the second involved only polynomial multiplication, which is a much faster process. On the other hand, the first method has no significant memory requirements while the second method requires sufficient memory to store the results for p(n+1) candidate polynomials. Clearly, neither method is tractable for GF(pn) fields of any significant size; in the case of our GF(75) field, we are talking about either 711 (2 billion) or 710 (~280 million) operations with the latter also needing to store 76 (~120 thousand) results. Although this is reasonably doable on modern PC's, if we increase the size of the field just a bit it would become infeasible even for all of the computing power likely to exist in the world for the foreseeable future.
Before we raise the white flag, let's explore what a bit of consideration can buy us. It's unlikely that we will reduce the complexity significantly, but we are very likely to gain a better appreciation for some of the basic properties of working with modular polynomials that we haven't seen to this point and that might come in handy later.
First, let's consider whether all of the possible p(n+1) candidate polynomials are really candidates at all. The first thing to note is that the coefficient of the Dn term can't be zero, otherwise we don't have a polynomial of degree n. The second thing to notice is that the constant term (coefficient of the D0 term) also can't be zero otherwise the polynomial would be divisible by D. In our GF(75) example, these two considerations alone eliminate more than one quarter of the candidates.
Next, let's examine the case when the coefficient of the Dn term is greater than one. Clearly this term is divisible by a constant term, but is the entire polynomial also divisible by this same constant term? The answer is yes, since dividing a polynomial by a constant term reduces to multiplying each term in the polynomial by the multiplicative inverse of that constant and since this operation is carried out in GF(p), the result will be a polynomial in the set. For example, consider the polynomial
5D5 + 3D4 + 6D2 + 4
This should be evenly divisible by 5. Performing the division by multiplying the polynomial by the multiplicative inverse of 5 in GF(7), which is 3, we obtain
D5 + 2D4 + 4D2 + 5
This result means that we only have to consider as candidates those polynomials that are of order n and that have a high order coefficient of exactly one and a non-zero constant term coefficient. There are O(pn) such polynomials. But the news is even better than that; we can greatly reduce the set of test divisor polynomials. As when attempting to factor an integer, we do not need to test every integer that is smaller, we only need to test those integers that are prime and that are smaller than the square root of the integer we are trying to factor. A similar rule applies here, we only need to test those polynomials that are irreducible and of order less than or equal to n/2. If we assume that all polynomials with a high order coefficient of one and a non-zero constant coefficient are irreducible and must be used as test divisors, this results in a complexity of O(p(3n/2)). This is still exponential, but it extends the range of fields for which the computations are feasible. For our GF(75) example, this reduces the number of polynomial division operations needed from two billion to less than one million. This can be reduced significantly further by adopting a recursive approach and building up a table of irreducible polynomials of lower degrees and then using only the irreducible polynomials as test divisors.
Turning our attention to the second approach, we can use many of the same lessons. First, we only have to store pn results, which reduces the memory requirements in our GF(75) example from 120 thousand results to only 17 thousand. Furthermore, we can work through the pairs of polynomials to be multiplied in a much more systematic fashion. We only need to consider pairs of polynomials where the products of the high order terms are Dn and, as a consequence of what we know about divisibility by constant polynomials, we can restrict both polynomials to those whose high-order coefficients are one. The number of multiplications that must therefore be performed is O(npn). In the case of our GF(75) example, this is on the order of eighty-five thousand and a more careful accounting actually places it at slightly less than twenty-five thousand polynomial multiplications. As with the first approach, this can be further trimmed by identifying the lower order irreducible polynomials and only considering them in the multiplications, although we must take care to include integer powers of them as well.
Assuming that we have obtained or generated a list of all irreducible polynomials of degree n, how do we determine which ones are primitive?
The only guaranteed way of doing this is to test it by seeing if all of the polynomials in the set, with the exception of the additive identity polynomial, can be generated from it.
Here are a couple of properties regarding primitive polynomials that we will use, but make no attempt to prove or even justify.
Let's see what this says about our GF(75) example. First, let's determine how many primitive polynomials there are.
Number of primitive polynomials = phi(pn − 1)/n
Number of primitive polynomials = phi(75 - 1)/5
Number of primitive polynomials = phi(16806)/5
Number of primitive polynomials = phi( (2)(3)(2801) )/5
Number of primitive polynomials = phi(2)phi(3)phi(2801)/5
Number of primitive polynomials = (1)(2)(2800)/5
Number of primitive polynomials = 1120
While there's no way (that I am aware of) to determine how many irreducible polynomials (of degree n) there are, we have previously determined that an upper limit on the number is 2058 )(1*7*7*7*6), so more than half of them are primitive. Keep in mind that this is merely an anecdotal result and is in no way meant to imply anything general.
The second property may not look useful, but in fact is quite handy for a couple of things. First consider the fact that, put another way, it says that
M*K = (Dm - 1)
Where M is our modulus polynomial and K is just some polynomial. This is directly analogous to the statement
p*k = (xm - 1)
when working in the mod-p world. Note that neither k nor K have to be elements in the fields. As in the mod-p world, we can reduce both sides to obtain
M*K
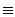(Dm
- 1)
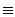0
(mod M)
Dm
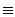1
(mod M)
But we also know that anything raised to the zero power is also congruent to the multiplicative identity, and hence
Dm
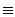D0
(mod M)
The requirement that this is true for no smaller value of m than (pn - 1) requires that every Dk for 0<k<m produce a different element of the set. We also know that, unless D is identically equal to 0, that Dk can never produce 0. Since there are pn elements of the set there are (pn - 1) elements that are different from 0 and since we have (pn - 1) different values of k to choose from, D must be a generator of the entire set.
So one way to determine if a particular M (irreducible polynomial of degree n) is primitive is to determine if D is, in fact, a generator of the entire set using that M. However, it is not enough to simply test if Dm is congruent to 1 (mod M), since it will be. But checks against the powers corresponding to the factors of m will give a good indication.
Instead of finding a primitive polynomial by brute for in our GF(75) world, we will use the Combinatorial Object Server from the University of Victoria. This tool indicates the following as being a primitive polynomial in GF(75)
105004 = D5 + 5D3 + 4
The bottom line, unfortunately, is that while we can make significant strides in reducing the number of operations required, the complexity of finding the primitive polynomials in a particular finite field is still exponential and therefore limited to relatively small finite fields. As stated before, for specific fields, most notably GF(2n), shortcuts have been developed to at least generate primitive polynomials of a particular degree.
We've already established that expressing the elements in GF(pn) is a viable and useful approach. What the previous discussion has shown is that each element, other than 0, can also be expressed as an integer power of D. This means that there is a one-to-one mapping between in first (pn - 1) powers of D and the non-zero polynomials in GF(pn). This, in turn, means that we can use either representation at will and switch back and forth between them as the situation warrants.
However, there is a catch. While determining which polynomial a particular power of D maps to is straight forward, the reverse is not the case. Given a polynomial in D, it is very difficult to determine which power of D it maps to by any means other than brute force enumeration. The reason for this is that we are looking for the solution to the following problem:
P = Da mod M
Where we have a polynomial P and want to find the exponent a. However, this is the discrete logarithm problem upon which the security of cryptographic protocols and systems such as Diffie-Hellman and RSA are based.
The fact that Dm
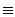1
(mod M) in our GF(pn) finite field gives us a very
powerful and efficient means of computing multiplicative inverses. If we want to
find the multiplicative inverse of D s then all we must do is
find D t such that
(Ds)(Dt) = Dm
Which means that
Dt = (Ds)-1 = D(m-s)
This is not to say that this has become easy, except in comparison to the alternatives. For instance, if we wanted to find the multiplicative inverse of D17, we could easily determine that the power we need to raise D to is 16779 since m is (pn-1) which is 16806. This may look completely daunting at first, but remember that we have the very powerful square-and-multiply technique for performing fast modular exponentiation.
There is one catch in this approach. While determining which polynomial a particular power of D maps to is straight forward, the reverse is not the case. Given a polynomial in D, it is very difficult to determine which power of D it maps to. The reason is that we are looking for the solution to the following problem:
P = Da mod M
Where we have a polynomial P and want to find the exponent a. However, this is the discrete logarithm problem upon which the security of cryptographic protocols and systems such as Diffie-Hellman and RSA are based.
http://en.wikipedia.org/wiki/Primitive_polynomial (Accessed 27 JUL 07)
http://www.theory.cs.uvic.ca/~cos/gen/poly.html (Accessed 27 JUL 07).