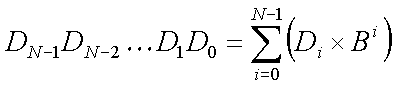
(Last Mod: 22 January 2012 13:56:11 )
Classical Positional Numbering Systems
Computer-based Number Representation
When you see the "number" 22 written on a piece of paper what you are really seeing is a symbolic representation that is intended to communicate an idea - namely the idea of the number twenty-two. Those two 2's sitting next to each other are not twenty-two of anything. Indeed, the very concept of "twenty-two" is an abstract one.
"So what?" you might ask. Indeed, most of the time there is no need to be so specific about the distinction - humans have an extremely well developed ability to take a symbolic representation and extract from it the concept that is being communicated. We do this automatically and it serves us very well, but it can get in our way when we need to focus on the representation itself separate from the concept that is being represented.
In this Module we do precisely that. So we will first make sure that the representation we use in everyday life is very well defined and understood. Then we will see how we can use those concepts as the foundation for new ways of representing numbers - ways that a computer can deal with.
For both our everyday numbering system and for computer-oriented representations, we will begin with how we represent positive integers. We will then extend this to include negative numbers and the to fractional values. Finally we will extend it to include extremely large and extremely small values.
Finally, after working through the various standard ways that numbers are represented, we will take a look at how text, both characters and strings of characters, can be represented.
Located at the very end of this material are two appendices. The first provides a brief review of integer and modulo division while the second reviews the basic properties of exponentials and logarithms. Both appendices include examples which are relevant to various programming tasks in this course.
In most situations we use the Hindu/Arabic numbering system. Unlike an additive numbering system such as the Roman Numeral, the Hindu/Arabic system is a positional numbering system. Like all but two of the widespread positional systems throughout history, it is a base-10 system. The Babylonians used a base-60 system - which we still have a remnants of in our units for time and for angular measure. The Maya used a base-20 system and are thought to be the first culture to use the concept of "zero" in representing numbers.
The basic idea behind a positional numbering system is to be able to represent a large range of quantities with a high degree of accuracy while using a relatively small number of characters. For instance, in our base-10 system, we can uniquely represent one million different values using only six characters. Another important feature is that the mechanics of performing arithmetic in a positional numbering system are straight forward and well-structured. Imagine having to describe how to multiply two values together that are written using Roman Numerals.
In a positional numbering system we need a selection of primitive symbols equal to the base. These symbols represent the integer values zero through one less than the base. These symbols are collectively referred to as the numbering system's "digits". Hence, in is a base-10 system, we need ten symbols - or digits - that represent the integers zero through nine. Given these digits, we can then represent numbers using a string of these digits in such a way that the value being represented not only depends on the digit used, but on that digit's position within the string. Hence, 1667 is not the same as 7616 even though both strings use the same digits the same number of times.
The rules that we use to construct the string of digits that represent a number and, conversely, to interpret a string of digits to determine what number is being represented, are quite straightforward. Most readers of this material have learned and internalized these rules over the past decade or more. But what has really been internalized are practical ways of applying the rules when working with base-10 numbers - and as proficient as someone might be at this, they may not have a sufficient grasp of the rules themselves in order to apply them to non base-10 numbering systems or systems that otherwise differ from the ones we use everyday. So our first task is to explicitly develop a set of rules that describes our everyday use of a positional numbering system before we proceed to discuss how these rules are applied to computer-based representations.
The most important rules for working with positional numbering systems are most clearly seen when applied to one of the most basic type of numbers - the nonnegative integers (i.e., the set {0,1,2,3,...}). This set is frequently referred to as the "whole" numbers.
A formal way of expressing what the value represented by a string of N digits (in any positive integer base, B) would be:
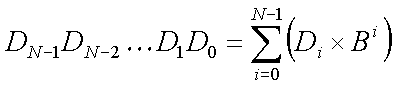
Here we have an N-digit number written in base B. The ith digit, Di, is one of the symbols representing the integer values {0..(B-1)}.
As a matter of verbal shorthand, we will generally use phrases like, "The digit '2' has an exponent of three." Taken literally, this would say that we have 23. What we really mean is that the digit '2' is multiplied by the number base raised to the exponent of three - or 2x103. But this is a lot of words that quickly get in our way and we simply agree that when we talk about a "digit" within a number "having an exponent" what we are referring to is the exponent that the base is raised to prior to multiplying it by that digit.
Given a string of digits that represent a nonnegative integer, we can determine the value that is represented by applying the most fundamental property of a positional numbering system embodied by the formal description above - namely that the position of each digit provides information as to how much "weight" that digit carries in the final result.
By way of example, consider the following:
k = 4532 (B=10)
D0 = 2
D1 = 3
D2 = 5
D3 = 4
k = 4x103 + 5x102 + 3*101 + 2*100
k = 4x1000 + 5x100 + 3*10 + 2
k = 4000 + 500 + 30 + 2 = 4532
The above should not come as any surprise, nor should the corresponding results when B is something other than 10.
k = 45326
D0 = 2
D1 = 3
D2 = 5
D3 = 4
k = 4x63 + 5x62 + 3*61 + 2*60
k = 4x216 + 5x36 + 3*6 + 2
k = 864 + 180 + 18 + 2 = 1064
Note that in this last example, the base was indicated in the original number by a subscript following it and that this is the only number that was written in the original base. In fact, had we written all of the numbers throughout the example in the original base, the results would have been identical to the earlier results because the number base is written as 10 in any number base. Note that this would include the number that represents the number base in the subscript itself. Hence you begin to see how tied we are to the decimal number system - even when writing a number in another base, we generally rely on the reader assuming that the base of the number is indicated in base ten.
When figuring out what value is represented by a string of numbers, we have the advantage of knowing what N is before we even start - we can count the the number of digits. When going the other way, determining what string of digits to use to represent a particular value, we generally don't have that piece of information. But it turns out that the steps needed to get it are not that much more difficult.
Consider the range of values that can be represented with an N-digit number, where we are assuming that the leading digit is something other than zero. The smallest value that can be represented is a 1 followed by (N-1) zeros. The largest value that can be represented is a string of N digits where each digit is the largest digit available. For B=10 and N=4, this would mean 1000 and 9999 respectively. Notice what happens if we add one to the upper limit. We end up with the first number that is too great to represent with an N-digit number and this number is easier to work with than the largest number that we can represent.
Using the above results, we can conclude that if k is an N-digit number that it obeys the following relationship:
B(N-1) <= k < BN
Note that this is actually two inequalities that just happen to be written in a single expression. In order for the expression to be true, both inequalities must simultaneously be true.
B(N-1) <= k and k < BN
So, given a value k that we want to represent in a number base B, how many digits are required? We can work with either inequality and solve for N. For simplicity, we will use the right hand expression:
ln(k) < N*ln(B)
N > ln(k)/ln(B)
Since N is an integer and it is strictly greater than the ratio on the right, all we must do is compute the right hand side and round it up to the next integer, even if it comes out to be an integer since, in that case, we must still add one to get a value for N that is strictly greater than the right hand side. Although technically we could use any value of N that is greater than the right hand side, doing so would violate the first inequality above except for the single value of N obtained by rounding up to the next integer.
Note that we could have taken the logarithms to any number base, as long as we were consistent. You should verify that you get the same result if you use common logs (i.e., base ten logs) as when you use natural logs.
You should be able derive a comparable result using the first inequality.
Once we know how many digits are in the number, we can determine the actual digits in a reasonably straightforward manner by successively finding each digit beginning with the most significant one (which is the left most digit).
If Di is the left most digit, meaning that i = N-1, then it there is a value for Di such that
(Di)xBi <= k < (Di+1)xBi
The value that satisfies the above relationship is the correct value for Di. To actually find the value of Di, you could use trial and error or divide k by Bi.
Having found Di for the left most digit, we note that we can now write our number as:
(DN-1)x(BN-1) + DN-2DN-3...D1D0 = k
Where we now have an unknown (N-1) digit number. Solving for this number, we have:
(DN-1)x(BN-1) + DN-2DN-3...D1D0 = k
DN-2DN-3...D1D0 = k - (DN-1)x(BN-1) = k'
We can now repeat the above process to find the left most digit in k' and then keep cycling though this process until we have determined all N digits.
The first issue to take care of is the notion of "significant digits". A significant digit is one whose presence is critical to the representation of the number. Consider the representation of "one dozen". Normally we would write this as:
n = 12
but we could also correctly represent this as:
n = 00000012
Since the presence or absence of the leading zeros does not alter the number being represented, they are considered "insignificant" and we can include them or not depending on what is convenient for our purposes at the time. In general through our discussions in this and later material, when we talk about the number of digits in a number we are referring to the number of significant digits.
While leading zeros (in an integer) are always insignificant, the same may or may not be true for trailing zeros. Given the number:
n = 12000000
The trailing zeros are significant only to the degree that they are a critical part of the value as opposed to simply being required for placekeeping purposes. For instance, if that number represents the exact result of the number of acres in a plot of land, then all of those zeros are significant. If, on the number hand, the number is an estimate of the number of acres that is accurate only to the nearest million acres, then none of the zeros are significant. Something in between these two extremes is also possible where the number might be an estimate to the nearest thousand acres in which case the first three zeros would be significant and the final three would not. Various ways of indicating which digits are and are not significant exist, such as placing an overbar above the nonsignificant zeros, but for our purposes it is sufficient to simply understand the basic concept of significant digits.
Let's say that we have fourteen gross of pencils (a gross is twelve dozen so fourteen gross is two thousand sixteen) and want to represent this number in base-8.
k = 2016
Let's first determine how many digits there are:
N > ln(2016)/ln(8) = 3.659 (so N=4)
We now want:
D3 = k / B3 = 2016/512 = 3.93 (so D3 = 3)
k' = k - D3 x B3 = 2016 - 3x512 = 480
We can tabulate these results, and the remainder of the results needed to determine all of the digits, in a table such as the following:
k = 2016
B = 8
N < ln(k)/ln(B) = 3.7 (N=4)
| i | k' | Bi | Di = int(k'/Bi) | Di x Bi |
| 3 | 2016 | 512 | 3 | 1536 |
| 2 | 480 | 64 | 7 | 448 |
| 1 | 32 | 8 | 4 | 32 |
| 0 | 0 | 1 | 0 | 0 |
In using the above table, the initial value of i is (N-1) and the initial value of k' is k. The rest of the values in the first row come directly from the first two. In moving to the next row, the value of i is decremented and the new value of k' is the old value (the value from the previous row) less the value in the last column (again, from the previous row). This process is continued until i is equal to zero. The digits of the final number are then easily retrieved from the 4th column. Note that the last value of k' must match the last value in the last column. In other words, k' on the next line (the line with i = -1) should be zero.
The final result is that fourteen gross is 37408.
To verify this result, we can use the properties discussed previously in how to determine the value represented by a number and we get:
k = 3x83 + 7x82 + 4*81 + 0*80
k = 1536 + 448 + 32 + 0 = 2016
Our basic system described thus far only permits us to represent nonnegative quantities. We could, in fact, get along without negative numbers - as countless generations in many civilizations did before us. But negative numbers add a great deal of power to our mathematical tool chest, and therefore we want to be able to represent them in a way that permits us tap that power.
In every day usage, we simply denote a negative number using a "-" sign in front of the number. But what is a negative number? Most people have long forgotten what the defining property of a negative number is. In short, we invoke the definition of an "additive inverse" whereby the sum of a number and its additive inverse is equal to zero. We refer to the additive inverse of a number as the "negative" of that number. If we look at the implication this has for how a number and its negative counterpart behave under the rules of addition and subtraction, we find a very natural way to represent negative numbers.
Let's say that A is a positive value and we want to find a way to represent quantity B, its negative. By definition, B is the additive inverse of A and hence we have:
A + B = 0
Solving for B, the number we want to represent, we find:
B = 0 - A
By invoking another property of arithmetic, namely the additive identity which states that C + 0 = C, we can write this simply as:
B = -A
So if A is 5, then its negative can be reasonably represented as -5.
It turns out that this representation, while intuitively straightforward and while it actually conveys quite a bit of information to us in a compact fashion, is actually pretty clumsy for performing arithmetic. For instance, consider the steps involved in simply adding and subtracting signed numbers. Our us of a minus sign to represent a negative quantity is so awkward to work with that we don't work with it! Instead, we use a fairly complicated set of rules to map it into a problem that can be performed using only positive quantities and then we either keep the final result positive or force it to be negative based upon which rule we invoked to perform the mapping.
As an example, if we want to subtract a larger number from a smaller number, we invoke a rule that says that we first subtract the smaller number from the larger number (and hence work only with nonnegative quantities) and then, because we noted that we were originally subtracting a larger value from a smaller value and therefore know that the result must be negative, we tack on the negative sign to the result. Take a moment and consider the various rules that you must use to simply add two numbers, either of which may or may not be negative. Pretty complicated - yet we do it without thinking much about it. We can get away with this because the human brain is amazingly powerful at internalizing complicated relationships and algorithms - if they make sense - given sufficient practice and repetition. Consider how we learn to play a musical instrument.
But computers are not good at this type of complicated rule processing - unless some human has sat down in carefully mapped out all of the rules and written very specific instructions for how to implement those rules. We therefore look for a way to represent negative quantities whereby we can perform arithmetic directly on them properly without having to invoke many, if any, special rules. We will hold off on discussing how we actually represent negative quantities in a computer because it involves a bit of sleight-of-hand that relies on a limitation of the range of values that can be represented by a computer - so it makes sense to delay this topic until these limitations are covered and understood.
While being able to represent integers is very important, there are certainly other values that we would like to be able to represent. For instance, how can we use a positional numbering system to represent fractional values such as the result of dividing five into one? First let it be said that we don't absolutely have to be able to do this at all and many cultures throughout history lacked a way of doing it using a positional numbering system. Instead, most of them simply tacked on some kind of fraction at the end of the integer portion to create what we commonly call a "mixed number" and this method is still in widespread everyday use today. It is more convenient for some things but less convenient for other things. By having more than one way to represent something, we gain the ability to use whichever method of representation better matches our needs at the time.
So, having decided that we would like to extend our positional representation so that it can represent fractional values, we look at the structure of our system and discover that a very simple means is staring us right in the eye. Looking at the pattern of what the digits represent, we see that power to which the base is raised decreases by one until we reach zero for the rightmost digit that serves as our units digit. What if we didn't stop there? The next digit would have an exponent of -1, the one to the right of that -2 and so on. Therefore, if we wanted to represent the quantity 5 and 3/4 using our positional system we use the same rules as before and produce the following:
The largest exponent needed is 0 (since 101 is larger than the number to be represented)
The first digit is 5 leaving a remainder of 3/4.
The next grouping size is 10-1 (1/10) and we can extract seven such groups leaving (3/4) - (7/10) = (1/20).
The next grouping size is 10-2 (1/100) and we can extract five such groups leaving nothing.
k = 5 3/4
B = 10
N < ln(5 + 3/4)/ln(10) = 0.76 (N=0)
| i | k' | Bi | Di = int(k'/Bi) | Di x Bi |
| 0 | 5 3/4 | 1 | 5 | 5 |
| -1 | 3/4 | 1/10 | 7 | 7/10 |
| -2 | 1/20 | 1/100 | 5 | 5/100 |
| -3 | 0 | - | - | - |
The resulting string of digits is 575 but immediately we see a problem. How can we distinguish this number from the quantity five hundred seventy five? Or fifty-seven and one-half? Or five hundred seventy-five one-thousandths? We need to know what the exponent actually is for at least one of the digits - after that we can easily determine what it is for any other digit since it increases by one as we move to the left and decreases by one as we move to the right.
We actually had the exact same problem when we were restricted to integers but the solution was so intuitive that we didn't need to explicitly point it out - it was simply understood that the rightmost digit had an exponent of zero. We could solve our problem by merely noting the exponent of either the leftmost digit or the rightmost digit off to the side and, as we shall see in a little bit, this is not so unwieldy as it might seem - in fact we use this method all the time.
But, for everyday quantities, there is a more convenient method. Instead of indicating what the exponent is for one of the two end digits, we simply agree to always do two things - (1) include the digit that has an exponent of zero, and (2) indicate which digit that is. To do the first, we may have to add leading or trailing zeroes to our string that otherwise might not be needed and to do the second we simply place a period to the right of the digit that has a zero exponent. Thus the quantity of five and three-quarters would be written as 5.75 using this convention. We normally call this period a "decimal point" but "deci" implies a base-10 numbering system and this method is equally applicable to any base. The generic term is "radix point".
Thus our expanded system is a very simple extension of our original one and we've really only added a single rule: If a radix point does not exist, then the rightmost digit has an exponent of zero (original rule). If a radix point exists, the digit to the left of it has an exponent of zero.
This method of representing fractional values is sometimes referred to as "fixed point" because the digit to the left of the radix point has a fixed value for the exponent.
Another way of creating a "fixed point" representation is to not place the radix point at all but work under an agreement where everyone knows where it would go if it were there. For instance, if I'm working with the federal budget I might not find it very convenient to have to write down twelve or so digits for each number. Instead, I might simply choose to leave off the last six digits from every number and, as long as I communicate that fact, then anyone reading my data knows that the decimal point is located six places to the right of the last digit shown. Another example is found in the standard format for conveying data for use in automatic machining processes. Here a common format is to present all values as a seven digit number and it is understood that the decimal point is located three places to the left of the last digit.
As stated previously, the fixed point method described above is quite convenient and suitable for most quantities we wish to represent in everyday usage. But it is not too convenient for representing very large quantities or very small quantities since we would have to include a large number of trailing zeroes in the former case and a large number of leading zeros in the latter. Either case is cumbersome and lends itself to making mistakes. So we need another extension.
Recall that previously it was stated that we could simply write the exponent of one of the digits off to the side. That's precisely what we'll do. Our new rule will be that we can take a fixed-point number and make what would normally be the units digit (the digit to the left of the radix point or, lacking a radix point, the rightmost digit) and assign it an exponent of our choosing. To indicate what that exponent is, we merely write it off to the side - normally the right-hand side. In order to avoid confusing this second number, called the "exponent", with the base number we started with, known as the "mantissa", we separate the two with a space or some other character. The most commonly used character is 'e' (for "exponent") but another common convention is to always include the sign of the exponent and make that character perform double duty by acting as the delimiter as well.
This notation is generally referred to as "exponential notation". Another name for it is "floating point" because the radix is no longer at a fixed location relative to the digit with a zero exponent. It is allowed to "float" and we simply keep track of where it has floated to.
Thus, a number like 123.45e5 means that the digit '3' actually has an exponent of five. The rest of the rules are unchanged and hence the digit '2' has an exponent of six and the digit '4' has an exponent of four.
There are a few ways of interpreting this notation. There is, of course, the way it was just described where the integer to the right of the 'e' is the exponent of the digit to the left of the radix point. This comes directly from our definition of this representation.
This representation is also commonly referred to as "scientific notation" but that is a bit of a misnomer. In scientific notation, the number is factored into two parts such that one of the factors is an integral power of the base. The power is chosen so that the other factor can be conveniently represented using the previously developed fixed-point radix notation.
So our number above could have been written as 123.45x105 in scientific notation. For completeness, we'll point out that in scientific notation the power is generally chosen so that the mantissa is "normalized" meaning that there is exactly one digit to the left of the radix point. Hence, in this example, the normalized representation would be 1.2345x107. In an alternative known as "engineering notation" the power is chosen so that it is a multiple of three which makes the use of scaling prefixes such as "milli" and "mega" more convenient. Our example might be expressed in engineering notation as 12.345x106.
Now, on the surface, it looks like the only difference between "scientific notation" and "exponential notation" is one of semantics. The "x10" is replaced by "e" and the exponent isn't written as a superscript. This slight change of notation allows us to type the numbers into a text file without needing any special characters for the exponent. So why do we claim that equating "exponential notation" and "scientific notation" is technically not correct? Because this similarity and ease of mapping is not intrinsic to the two representations - it is the result of a very deliberately chosen convention.
To see what is meant by this let's, for the moment, assume that we had chosen a different convention for our exponential notation. Let's specify that the mantissa would always be written as an integer and the number to the right of the delimiter is the exponent of the leftmost digit. In that case, the number we have been working with above would have been written as 12345e7. This convention actually has some advantages over the accepted convention, such as making it very easy to order a list of numbers. Had this, or another, convention been adopted we would have gotten used to and learned how to convert between exponential and scientific notation just as we have learned how to convert between fixed-point and scientific notation. But, just as mistakes are commonly made in translating between fixed-point and scientific notations, it would have been common to see mistakes made when translating between exponential and scientific. The people that developed the accepted convention for exponential notation recognized that having the exponential notation be equivalent to scientific notation for all practical purposes would minimize these translation errors and that this constituted a much stronger advantage than any of the other conventions might have had.
The purpose of this digression is twofold:
First, it points out the distinction between the "definition" of something and the "properties" of that same thing. The definition is what actually establishes what the thing is. It is generally expressed in the shortest, clearest terms possible. The "properties" of something are merely consequences of the definition, but the properties do not define it. In our case, a working definition of the exponential notation could be as simple as: Take a fixed point number and move the radix point to any convenient location within the number. Then append a delimiting character and the exponent of the digit to the immediate left of the radix point. Given this specific definition, our exponential representation has some interesting and useful properties - properties that it would not have if the definition has been different. For instance, because the digit to the left of the radix point would normally have had an exponent of zero, there are a couple of other interpretations that become useful. One is to think of the value to the right of the 'e' as the value that is added to the normal values of all of the exponents in the original fixed-point value. In the number above, 123.45e5, the digit '1' normally would have an exponent of two, so five is added to this, and it now has an exponent of seven. Likewise, the '5' would normally have an exponent of negative two and therefore now has an exponent of positive three. Another very useful way of thinking about the representation is that the mantissa is multiplied by the number base raised to the indicated exponent. In the number above, this means that we have 123.45 x 105 and hence the intentional behavior that exponential notation maps very easily to scientific notation.
Second, it emphasizes that there is nothing rigid about number representation. If we decide that we would be better off using a different definition for the exponential notation, then we are completely free to do so. Keep in mind that if we ever need to communicate values to someone else, we will either have to go to the effort of making it clear that they understand how to interpret our representation or we will have to convert to one of the commonly accepted representations. But if we only intend to use our custom representation for internal computations, then by all means we can feel free to develop a representation that best suits our needs - we just need to be consistent in its use. In developing a custom representation, it is very useful to keep in mind the difference between the "definition" and the "properties" of our representation. Doing so will make it much easier to ensure that yur representation is adequately defined and that we use it consistently.
Following up further on the closing remarks of the previous section, hopefully you have noticed a strong thread running throughout this discussion. When representing numbers, there is nothing mystical or magical about them and there are several representations we use in normal everyday life. The reason why more than one exists is because no single representation is perfectly suited for all numbers or, more importantly, for all applications involving those numbers. So we have developed a handful of representations and we choose the one that is best suited to our needs at the time.
Furthermore, it is not uncommon at all to switch back and forth between different representations in the process of performing a given task. For instance, in constructing a roof truss we might write the measurements taken with a tape measure in mixed notation using fractional inches, add a few of them together this way, then convert them to decimal inches to plug them into some formulas, and then convert them back to mixed notation when it comes time to lay out the resulting lines on the lumber to be cut.
Two lessons should be drawn from this:
First, working with different representations and converting between them is something we do all the time, but it is not natural to us. We learned how to do it and spent a considerable amount of time, effort, and practice to develop the necessary skills. For similar reasons, we will find that having a few different methods of representing numbers within a computer is very convenient and that we will need to be able to convert back and forth between them. It should therefore not come as a surprise that becoming conversant with how to do these conversions will require some time, effort and practice.
Second, how a number is represented should be driven by the number itself combined with how that number is going to be used. It should not be driven solely by a reluctance to choose a proper representation from among the many that are available. Furthermore, we should not even restrict ourselves to just the ones that are available. Remember that we have more than one because no single one is perfectly suited to every occasion. The same is true for the collection of representations available to us. They are highly flexible, but it is expecting too much to insist that one of them is perfectly suited to every occasion. If your needs argue for using a custom notation, then use a custom notation. You just need to be sure that your notation is up to the task at hand and that you use it consistently.
When we write a number, we need to be sure that the number base used is clearly understood. In every day life we almost always work with decimal value (base-10) and hence don't worry about indicating this - it is simply understood by everyone as the assumed number base.
But when we work in other bases we need to be more careful. Sometimes the context of the discussion makes it clear what the number base in use is, but if there is any chance for miscommunication then we need to be more explicit. The most common way of indicating the number base used for a specific number is to follow it with a subscripted value, written in base ten, indicating the base. Sometimes this is inconvenient or even impossible since text files do not support the use of subscripts. In that case we need another way to represent the value.
For our use, we will either follow the value with a subscript indicating the base or, alternatively, use the following notations:
| Base | Name | Digits | Notation | Example of Representation |
| 2 | binary | 0,1 | Suffix with 'b' | 1110 1111b |
| 10 | decimal | 0...9 | (none) | 96 |
| 16 | hexadecimal | 0...9,A...F | Suffix with 'H' | 5FH |
| 16 | hexadecimal | 0...9,A...F | Prefix with '0x' | 0x5F |
Notice that there are two common alternate notations for hexadecimal. We will predominantly use the '0x' prefix because this is the notation used by the C programming language.
In the case of binary numbers, we will generally write the value in groups of four digits. The purpose is simply to make the value easier to read - the space has no impact on the value at all just as we commonly use commas to group a base ten number into groups of three digits.
There are times when we need to convert the representation of a number in one base to a different base. It's important to understand that we are not changing the value of the number represented, only the representation itself.
There are two obvious ways to accomplish base conversion that follow directly from the concept of what a positional number system is.
The first is to go through digit by digit and multiply it by the appropriate weight for that digit's position and sum up the result. If the arithmetic is performed in the target number base, then the final result will be in that base. Here the arithmetic is performed in the base of the number system being converted to and hence this is the most common way to convert from an arbitrary base to decimal because we are comfortable performing the math in base-10. It is not a common way to convert from decimal to another base for the simple reason that few people are comfortable performing arithmetic in any base other than base-10.
6357 = 6 x 72 + 3 x 71 + 5 x 70 = 6 x 49 + 3 x 7 + 5 x 1 = 32010
The second way to convert is to build up the number in the new base following exactly the steps introduced earlier - namely to figure out the weight of each position and figure out how many groupings of that weight can be removed from the number and proceed digit by digit until the units digit is reached (or further if something other than an integer is being converted). Here the arithmetic is performed in the base of the number system being converted from and hence this is the most common way to convert from decimal to an arbitrary base because, as above, we are comfortable performing the math in base-10. Similarly, it is not a common way to convert from another base to decimal.
70 = 1
71 = 7
72 = 49
73 = 343
Since 49 <= 320 < 343, the number in base-7 has three digits.
Dividing 320 by 49 yields 6.53 and so the there are six complete groupings of 49 in 320. The first digit is therefore '6'.
Subtracting off 6 x 49 = 294 leaves a remainder of 26 to be represented by the remaining two digits.
Dividing 26 by 7 yields 3.71 and so there are three complete groupings of 7 in 26. The second digit is therefore '3'.
Subtracting off 3 x 7 = 21 leaves a remainder of 5 which is the remaining digit.
So the result is 6357.
As indicated, the two methods described above are "brute force" methods and they always work - but they are not the only two methods. The fact that they are the most common is not a tribute to their efficiency, but merely to the fact that they are almost always the only two methods that are taught. As the saying goes, when the only tool you have is a hammer, everything looks suspiciously like a nail. So let's add a couple of tools to our toolkit - there are alternate methods that, with just a little bit of practice, enable much quicker conversions. These conversions, in the form presented, are limited to converting integers. But converting fixed-point and floating-point can be done by applying a bit of finesse, as we shall see later.
The first of these is repeated multiplication by the number base being converted from with the arithmetic being performed in the number base being converted to - hence this method lends itself to conversions to decimal from another base. The basis for this method becomes apparent by noting the following:
6357 = 6 x 72 + 3 x 71 + 5 x 70 = 6 x 7 x 7 + 3 x 7 + 5 = 7( 7(6) + 3 ) + 5 = 32010
To better see the systematic approach embodied by this method, consider the algorithm for using it:
To convert a number from an arbitrary base to decimal:
Step 1: Initialize "result" to zero
Step 2: Start with the left most digit as the "present digit"
Step 3: LOOP:
Step 3.1: Multiply "result" by the number base
Step 3.2: Add the "present digit" to "result"
Step 3.3: Make the next digit to the right, if there is one, the new "present digit"
Step 3.4: WHILE there is a new "present digit", continue the loop (i.e., go to Step 3.1)
If you walk through the above algorithm you will notice an inefficiency that is embedded in it. The first time through the loop you start with "result" equal to zero and you first multiply this by the number base - seven in our case - and then add the leftmost digit. Why not simply initialize "result" to the leftmost digit in the first place? You can and, when doing the conversion manually, you almost certainly will. But if you were encoding this algorithm into a computer program your algorithm has to be explicit about every step and the shortcut we would naturally use manually requires quite a bit more thought to explain it properly in a step-by-step algorithm. We could do it, and perhaps pick up some performance in the process, but it is generally better to keep your algorithms as simple as possible even if it is at the expense have having some steps whose effect is wasted from time to time.
Solution: Let's assume that it has been awhile since we've done a conversion and all we remember is that we walk across the number digit by digit and that we multiply our partial result by the number base each time we add one of the digits. But we don't remember if we go from right to left or from left to right. Also, we aren't sure when we start and stop multiplying by the number base. If our knowledge of how to use this method was based strictly on memorizing a bunch of steps, we would be stuck. But since our knowledge is based instead on understanding why the method works, we can quickly figure it out. For instance, we know that you can't multiply the result by the base after adding in the unit's digit because the unit's digit represents single quantities. Therefore we have just determined that we go from left to right and that we multiply by the base after adding in each digit except for the last one.
6
x8
--------
48
+3
========
51
x8
--------
408
+4
========
412
x8
--------
3296
+7
========
3303Result: 63478 = 330310
The second alternate method is basically the inverse of the method above and uses repeated division by the number base being converted to with the arithmetic performed in the number base being converted from - hence this method lends itself to conversions from decimal to another base.
Using the example above once more, to convert 32010 to base-7, we divide by the new number base, 7, and get
320 / 7 = 45 r 5 (45 with a remainder of 5), hence 5 is the last (i.e., rightmost) digit. Proceeding with just the whole part of the result, we have:
45 / 7 = 6 r 3, so 3 is the second digit from the right. Again proceeding with just the whole part of the result, we have:
6 / 7 = 0 r 6, and so 6 is the third digit from the right and since the whole part is now zero, we are finished.
A common way of writing this when converting by hand is:
7 | 320
7 | 45 r 5
7 | 6 r 3
7 | 0 r 6
The converted number is simply the remainders starting with the last one first, or 6357 in this example.
As with the previous method, this one also lends itself to a compact algorithm:
To convert a number from decimal to an arbitrary base:
Step 1: Initialize "quotient" to the original number being being converted
Step 2: Start with "result" being completely blank (no digits)
Step 3: LOOP:
Step 3.1: Divide "quotient" by the new base with the result expressed as a new whole number "quotient" and a "remainder"
Step 3.2: Tack on the "remainder" to "result" as the new MSD (Most Significant Digit or leftmost digit).
Step 3.3: WHILE "quotient" is larger than zero, continue the loop.
Use the above algorithm to make the conversion of 320 from base-10 to base-7.
Step 1: quotient = 320
Step 2: result = 0
Step 3.1: 320/7 = 45 r 5 so quotient = 45 and remainder = 5
Step 3.2: result = 5
Step 3.3: Since (quotient > 0), go back to Step 3.1
Step 3.1: 45/7 = 6 r 3 so quotient = 6 and remainder = 3
Step 3.2: result = 35
Step 3.3: Since (quotient > 0), go back to Step 3.1
Step 3.1: 6/7 = 0 r 6 so quotient = 0 and remainder = 6
Step 3.2: result = 635
Step 3.3: Since (quotient = 0), we are finished.
Check the calculation of the exercise in the previous section by converting 3303 to base-8.
Solution: Again let's assume that it has been awhile since we've done this type of conversion and we want to make sure we do it right. Here the issue is whether our string of remainders are the digits in the result from left-to-right or right-to-left. If we ask what happens if we change the number by one, then we know that the result should only change by one. Now we ask which of the remainders is affected by a change of one and the answer is the first one. So the first remainder is the right most digit.
3303 / 8 = 412 r 7
412 / 8 = 51 r 4
51 / 8 = 6 r 3
6 / 8 = 0 r 6Result: 330310 = 63478
The method introduced above for converting decimal integers to another base using repeated division is, with practice, considerably quicker than using the brute force method. But it has two drawbacks if you are trying to speed up the process by using a calculator to perform the arithmetic. First, the division results are, on most calculators, presented only as a single number with a decimal fraction. So we must convert this decimal fraction to an integer numerator either mentally or by multiplying just the fractional part by the new number base. But this generally requires having to lose the whole number portion of the division result which is needed to continue the conversion. The result is that we have to store and retrieve intermediate results, either mentally, on paper, or in the calculator's memory, and the process is a bit cumbersome let alone affected by the individual and the capabilities of the calculator in use.
But there is another way to perform this task that uses repeated multiplication, albeit is a different fashion than is used to convert a value from another number base to decimal. To set the stage for how this method works, let's first look at a three digit decimal number and see how we could isolate the individual digits.
123
If we divide by the number base, ten in this case, enough times to get a result that is less than one, we would need to do so three times and end up with:
0.123 (after dividing by ten three times)
If we multiply by ten, we get
(0.123) x 10 = 1.23
The whole number part is the first digit. If we then remove the whole number part and multiply by ten again, we get:
(1.23 - 1) x 10 = 2.3
Now the whole number part is the second digit. If we repeat this process again, we get:
(2.3 - 2) x 10 = 3
If, instead of dividing by ten three times and then multiplying by ten three times we were to use a different base then the whole number parts that would have been revealed after each multiplication would have been the successive digits of the number as represented in the base used.
An informal proof that this is true is quite straightforward. Consider that we have a number x and we want to recover the digits of that number in an arbitrary base, b. Based on our definition of a positional numbering system, this string of digits (sticking with a three digit example) would be:
x = A x b2 + B x b1 + C x b0
By dividing by b three times (two is actually sufficient, but three is more systematic) we have:
x / b3 = A / b1 + B / b2 + C / b3
If we now multiply by b, we get:
A + (B / b1 + C / b2)
Keeping in mind that A, B, and C are all integers strictly less than b, we see that the above value, represented in any number base, will be have A as the whole number part and the term in parentheses as the fractional part. If we now subtract A (after recording it elsewhere as the first digit of our base-b representation) we are left with
B + (C / b1)
Now B is the whole number portion and we repeat the same procedure as above, leaving use with:
C
From a practical standpoint, the benefit that this method has is that intermediate results don't need to be stored away and then recalled in order to determine the value of the current digit. The current digit is simply the whole number portion of the intermediate result (displayed in base ten, or more correctly, in the base of the original representation). This quantity is readily identifiable and can be recorded elsewhere as part of the new representation and then can be easily subtracted from the present result. Hence this method is extremely streamlined for either hand conversions or calculator-assisted conversions.
First, divide by eight enough times to yield a result that is less than one:
3303 / 8 = 412.875
412.875 / 8 = 51.609375
51.609375 / 8 = 6.451171875
6.451171875 / 8 = 0.806396484375
Since we had to divide by eight four times, we will need to multiply by eight four times and will end up with a four digit number in base-8. At each stage, we subtract off the whole number portion before proceding:
0.806396484375 * 8 = 6.451171875
0.451171875 * 8 = 3.609375
0.609375 * 8 = 4.875
0.875 * 8 = 7
Result: 330310 = 63478 (which agrees with our earlier example using repeated division)
Conversions between hexadecimal and binary are extremely simple - which is one of the reasons that hexadecimal is so widely used in fields related to digital technology. Each hexadecimal digit maps directly to four binary bits and each four binary bits map directly to one hex digit. This property can frequently be exploited to make conversions quicker and less prone to mistakes. For instance, when converting from decimal to binary (or vice-versa) it is generally easier to convert to hex first.
This same property applies to base-8 (known as "octal") as well, except here each octal digit maps directly to three binary digits.
Example: Convert 63478 (the result from a prior example) to hexadecimal
Solution: Normally when converting between two non-decimal bases, we would convert to decimal as an intermediate step so that our arithmetic can be performed in decimal. But here we can use binary as our intermediate step and avoid arithmetic altogether!
63478 = 110 011 100 111
Regrouping into groupings of four:
110 011 100 111 = 1100 1110 0111
Converting each group to hex:
1100 1110 0111 = 0xDE7
Final Result: 63478 = 0xDE7
Check: Converting this to decimal yields 3303 which agrees with the original example.
Although the above methods were developed for converting integers, we can use them to convert non-integer values by simply scaling the number to be converted appropriately before converting it, then scaling it back to its original value. We can even avoid this overhead if we use the method of repeated multiplication taking care to keep track of the radix point, which is the method we will develop first. Regardless of what method we use, we must be aware that we need to convert the proper number of digits beyond the radix point to preserve the level of accuracy contained in the original value.
For now, let's focus on the two repeated multiplication techniques. Converting from base-10 to another base is the simplest because we must do nothing extra beyond keeping track of when we reach the radix point. Other than that we can continue converting digits as long as we desire. When converting to base-10, we must hold off on dividing by the other number base until we have the value converted over to base-10 (since we want to perform the division in base-10 and not the original number base). So while we can continue converting digits beyond the radix point for as long as we chose, each one involves an extra multiplication by the original number base that we must eventually divide back out.
We must divide the original value by the new number base twice to get a value less than one:
13.14 / 5 = 2.628
2.628 / 5 = 0.5256
The first two multiplications we perform will get the whole number portion of the final result:
0.5256 * 5 = 2.628
0.628 * 5 = 3.14
Any subsequent multiplications will reveal successive digits to the right of the radix point:
0.14 * 5 = 0.7
0.7 * 5 = 3.5
0.5 * 5 = 2.5
0.5 * 5 = 2.5
We can continue this as far as we would like and, when we reach the point at which we wish to stop it is easy to see if the last digit should be rounded up or not. In this case, it should. So, to four radix places, our have:
Result: 13.1410 = 23.03235
2
x5
--------
10
+3
========
13 <-- Whole number portion
x5 (extra multipication)
--------
65
+0
========
65
x5 (extra multipication)
--------
325
+3
========
328
x5 (extra multipication)
--------
1640
+2
========
1642
x5 (extra multipication)
--------
8210
+3
========
8213Since we multiplied by five and extra four times, we must now divide by five four times:
8213 / 54 = 13.1408
Result: 23.03235 = 13.140810
Note that, in either technique, we could have separated out the original whole number and fractional parts and converted them separately before combining them back into a final result. Doing so would be particularly attractive if doing all the computations by hand.
Also note that we did not recover the exact value that we started with in the prior example. This should not be surprising since we had to round the result in the prior example and, since we rounded up, we could have anticipated that our result in the second example would end up a little larger than our original starting value. In general, the issue of rounding and how many digits should be converted is one that we must deal with, in some way, when we convert a non-integral value from one base to another.
Just as we could use determine how many digits a certain integer requires when represented in a different number base, so too can we easily determine how many digits we need to have to the left of the radix point to correspond to a desired accuracy. Consider our original value in the prior examples, namely 13.14. One way to look at this number is to assume that it is accurate to within one-half of it's last digit since any value greater than or equal to 13.135 and less than 13.145 would have been expressed as 13.14. If we convert this value to another number base and then convert it back, we want to be assured that we at least get a value that falls somewhere within this range. We can do this as long as the least significant digit in the new base can has a resolution smaller than this total range of 0.01.
Hence:
1 x b2-n < 1 x b1-m
Where:
b1 is the base we are converting from
b2 is the base we are converting to
m is the number of digits to the right of the radix point of the number in the old base
n is the number of digits to the right of the radix point of the number in the new base.
Solving for n yields:
n = m log(b1)/log(b2)
So to preserve the level of accuracy represented by the decimal value of 13.14, we need
n = 2 log(10)/log(5) = 2.86
We need to always round this value up to the next higher integer, so we need three digits beyond the radix point in our base-5 number.
A slightly different approach that some people might find more intuitive and, at least under some circumstances, easier to use is to scale the number being converted both before and after the conversion in such a way that the number that is actually converted is an integer. This permits us to use any of the techniques already developed for the conversion of integers without any modification at all.
The mathematical basis for this method is as follows:
x = (bn * x) / bn
Which simply recognizes that if we both multiply and divide one value by another that we have not changed the value. If x is a real value with a fractional component that we want to preserve in our conversion, then we only have to multiply by a sufficiently large value of bn to ensure that integer portion of it contains all of the significant information. For instance, if we want to convert 3.14 to some other base, then we can multiply it by 102 (since we want to preserve two base-10 radix places) and convert the integer 314 to the other base. We must then divide by one hundred and this might be difficult since it must be done in the other base - a base that we are almost certainly not comfortable performing arithmetic in.
The key to making this conversion technique convenient is to notice that it doesn't matter what the exact value is that we multiply by (since we will be dividing by that same value later) as long as it is large enough. In the above example of 3.14, this means that 102 is merely the smallest value we can use. In particular, notice that it doesn't matter which value of b we use - the base we are converting from or the base we are converting to. But, whichever one we choose, we must multiply/divide by that number in both bases - once before the conversion and once after. Doing so in base-10 is straight forward regardless of which value of b we choose, but doing so in the other base is only convenient if we do so in that number base. The reason for this is that multiplying and/or dividing a value by an integer power of the number base in which it is represented is accomplished by the simple act of shifting the radix point the appropriate number of places to the left or right. Hence, to make things simple, we will always use the non-base-10 value of b.
We want to preserve two decimal digits (to the right of the decimal point) so our scaling factor must be larger than 102. We can either use trial-and-error to find a value of n such that 6n>102 (and, most often, this can be done very quickly) or we can be explicit and solve for n:
n = 2 log(10)/log(6) = 2.57 (need n = 3)
The value we will convert will then be:
k = 63 * 3.14 = 678 (rounding to the nearest integer)
Converting this to base-6 by Repeated Multiplication:
678 / 6 = 113
113 / 6 = 18.83333
18.83333 / 6 = 3.1388889 (partial result: 3)
Taking the manual shortcut where we only divide until the whole number portion is easy to convert, we now work back:
0.1388889 * 6 = 0.83333333 (partial result: 30)
0.83333333 * 6 = 5 (partial result: 305)
0 * 6 = 0 (partial result: 3050)
Now all we must do is divide by 63 which is accomplished merely by moving the radix point three places to the left.
Result: 3.1410 = 3.0506
In this example we don't need to spend any time determining what our scaling factor will be - we want to multiply by at least 62 in order to preserve the two radix places and so that is the value we will use.
The value we will convert will therefore be:
k = 62 * 3.056 = 3056
Converting this to base-10 by Repeated Multiplication:
((3 * 6) + 0)*6 + 5 = 113
Now all we must do is divide back out the fact of 62:
113 / 62 = 113 / 36 = 3.139
Result: 3.0506 = 3.13910
We are looking for an integer M such that
π = M / 164 => M = 164 x π = 205,887
Converting this to hex using any method of our choosing we get
M = 0x3243F
Result: π = M / 164 = 0x 3.243F
A similar approach can be used for working with numbers represented in an exponential format by first scaling the number to convert the exponent and then scaling the mantissa as above.
Example: Convert the number of electrons in a Coulomb to hex maintaining an accuracy of 0.1%.
Solution: charge on one electron = 1.602 x 10-19 C, so it takes 6.242 x 1018 electrons to get 1 C of charge.
My final value, in hex, is going to be of the form
value = A.BCD x 16E
Where A is a single non-zero hex digit in order for the value to be normalized. This means that:
A.000 x 16E <= (value = A.BCD x 16E) < 1.000 x 16E+1
Using the right-hand inequality, we can find the value of the exponent:
value < 1.000 x 16E+1
E + 1 > ln(value) / ln(16) = ln(6.242 x 1018) / ln(16) = 15.6
E = 15 = 0xF
We now use this to determine the mantissa that needs to be converted:
value = mantissa x 16E
mantissa = value / 16E = 6.242 x 1018 / 1615 = 5.4141
If we want to preserve this value to at least 0.1%, and since our method of conversion is to multiply by the new number base enough times to make this an integer, then we need to multiply by Bn such that:
1 < 5.4141 x 0.1% x Bn
Solving for n we get
n > ln [1/(5.414 x 0.1%)] / ln(16) = 1.9
n = 2
So the integer that we convert from decimal to hex is
M = 5.414 x 162 = 1386 = 0x56A
Dividing this by 162 and combining with the exponent yields a final result of:
0x 5.6A e F
As with the integer representations, moving between hex and binary is straightforward even when working with floating point values, although you must take care to make the necessary adjustments if you desire to keep the value normalized. We must recognize, however, that we can't just simply convert the exponent from hex to binary because what the relationship really means is that:
b.bbb x 2e1 = h.hhh x 16e = h.hhh x 2(4 x e)
So the exponent in the binary representation is four times the exponent in the hex representation. But this is easily accomplished by converting the hex representation's exponent to binary and shifting the result to the left two places.
Example: Convert the result from the previous example to a normalized binary exponential representation.
Solution: We can map from hex to binary directly, although the result may not be normalized.
0x 5.6A e F = 0101 . 0110 1010 e 11 1100 b
To normalize this, we must divide the mantissa by four (22) and add two to the exponent.
0x 5.6A e F = 1.0101 1010 10 e 11 1110 b
Converting from binary to hexadecimal is just as straightforward. First you multiply the mantissa by the power of two needed to make the exponent evenly divisible by four - meaning that the exponent's two least significant bits are zero. Then translate the result directly to hexadecimal.
Example: Convert the binary value 1.1001 0010 0001 1111 1011 01 e 1 to decimal.
Solution: First, we'll convert it to hex by multiplying the mantissa by two:
11.0010 0100 0011 1111 0110 1 e 0
Now we'll convert directly to hex:
value = 0x 3.243F68 e 0
To convert this to binary, we'll first make it an integer by multiplying by 166:
M = 166 x value = 0x 324 3F68
Converting this to decimal by the method of repeated multiplication yields
M = 52,707,176
To get the final value, we then divide this by 166:
value = 3.1415925
To perform most arithmetic operations, such as addition and multiplication, in a positional numbering system you must understand two concepts - first, how those operations are carried out on single digit numbers and, second, how those operations, when carried out on the component digits of a multi-digit number, interact with the operations on neighboring digits. For example, when adding two multi-digit numbers, add the corresponding digits of the two numbers, starting from the right, and invoke the concept of a "carry" from one position to the next.
When you were first learning to do addition and multiplication, you had to memorize your addition and multiplication tables at least through 9+9 and 9x9 (and usually a bit higher). Few of you have any need to look up the result of 6x8 any more and do not even realize you are recalling a memorized fact - one that you probably spent quite a bit of time and effort to commit to memory back in grade school. But the fact remains that you are still referring to an addition and multiplication table, it just happens to be one that you have long since internalized.
If you are going to work with numbers in bases other than base-10, you will need to have access to the addition and multiplication tables for single digit quantities in those bases. If you work in those bases enough, it will be worthwhile to commit those tables to memory. But in the meantime it is perfectly reasonable to refer to those tables when needed. It is, however, pretty important that you understand what those tables are - which means that you should be able to produce those tables, from scratch, without difficulty.
Let's construct the tables for base-8 (also known as "octal"):
Base-8 Addition Table
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 |
| 1 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 10 |
| 2 | 02 | 03 | 04 | 05 | 06 | 07 | 10 | 11 |
| 3 | 03 | 04 | 05 | 06 | 07 | 10 | 11 | 12 |
| 4 | 04 | 05 | 06 | 07 | 10 | 11 | 12 | 13 |
| 5 | 05 | 06 | 07 | 10 | 11 | 12 | 13 | 14 |
| 6 | 06 | 07 | 10 | 11 | 12 | 13 | 14 | 15 |
| 7 | 07 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
Base-8 Multiplication Table
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 00 | 00 | 00 | 00 | 00 | 00 | 00 | 00 |
| 1 | 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 |
| 2 | 00 | 02 | 04 | 06 | 10 | 12 | 14 | 16 |
| 3 | 00 | 03 | 06 | 11 | 14 | 17 | 22 | 25 |
| 4 | 00 | 04 | 10 | 14 | 20 | 24 | 30 | 34 |
| 5 | 00 | 05 | 12 | 17 | 24 | 31 | 36 | 43 |
| 6 | 00 | 06 | 14 | 22 | 30 | 36 | 44 | 52 |
| 7 | 00 | 07 | 16 | 25 | 34 | 43 | 52 | 61 |
The values were written as two digit numbers, using a leading zero where necessary, purely for consistency. The two tables can be combined into one by the simple expedient of placing both results in each cell separated by a space or a character. We'll use a forward slash and place the addition result to the left and the multiplication result to the right.
Base-8 Combined Addition/Multiplication Table
| +/x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 00/00 | 01/00 | 02/00 | 03/00 | 04/00 | 05/00 | 06/00 | 07/00 |
| 1 | 01/00 | 02/01 | 03/02 | 04/03 | 05/04 | 06/05 | 07/06 | 10/07 |
| 2 | 02/00 | 03/02 | 04/04 | 05/06 | 06/10 | 07/12 | 10/14 | 11/16 |
| 3 | 03/00 | 04/03 | 05/06 | 06/11 | 07/14 | 10/17 | 11/22 | 12/25 |
| 4 | 04/00 | 05/04 | 06/10 | 07/14 | 10/20 | 11/24 | 12/30 | 13/34 |
| 5 | 05/00 | 06/05 | 07/12 | 10/17 | 11/24 | 12/31 | 13/36 | 14/43 |
| 6 | 06/00 | 07/06 | 10/14 | 11/22 | 12/30 | 13/36 | 14/44 | 15/52 |
| 7 | 07/00 | 10/07 | 11/16 | 12/25 | 13/34 | 14/43 | 15/52 | 16/61 |
With the aide of this table, and the rules for how we carry out multi-digit addition, subtraction, multiplication, and division that we are already familiar with for base-10 we can now perform arithmetic directly in base-8. This is not to say that we won't find ourselves a bit rusty and perhaps a bit too reliant on calculators to make it very comfortable to perform the arithmetic directly at first. But our goal here is not to do enough arithmetic directly in another base so as to be comfortable doing it. Our goal is to do enough so that we reacquaint ourselves with the fundamentals of how to do it directly so that when it comes time to develop algorithms that have these fundamentals at our disposal.
Example: Multiply the base-8 numbers 53 and 27 performing all of the arithmetic directly in base-8.
53 53 53
x27 x 7 x 2
=== === ===
455 25 (3x7) 6 (3x2)
126 43 (5x7) 12 (5x2)
==== === ===
1735 455 126Result: 53 x 27 = 1573 (in base-8).
Example: Confirm the previous result by dividing 27 into 1735 directly in base-8.
First we'll make a little table of the products of the divisor and each of the possible digits.
27 27 27 27 27 27
x2 x3 x4 x5 x6 x7
=== === === === === ===
16 25 34 43 52 61
4 6 10 12 14 16
=== === === === === ===
56 105 134 163 212 241
53
------
27 / 1735
-163
------
105
-105
------
0Result: 1735 divided by 27 is 53 (in base-8) which verifies our prior result.
In the overwhelming majority of computers, values are stored in Base-2, also known as binary. The reason for this is simple - the circuits necessary to store and access one of two possible values from each memory cell are simple, small, and easy to build upon. As a result, the natural number base to represent integers and other values in a computer is Base-2.
But this is not a convenient number base for humans to work with because even reasonably small values require a lot of digits to represent - for instance it requires ten digits just to represent the number one thousand - and with only two different symbols humans are very prone to make mistakes even in just transcribing a number from one place to another.
It would be possible for humans to always work in the familiar Base-10 and convert numbers back and forth between binary and decimal representations when needed and, in fact, we do this a great deal. But there are many times when we need to work at a level very close to the actual representation and the sheer number of conversions would become daunting and error prone. What is needed is a compromise - a number base that allows rapid conversions between it and binary but that has a sufficient number of symbols to permit humans to develop a reasonable utility in manipulating it - if for no other reason than to minimize transcription errors.
For a long time, the accepted number base was Base-8, also known as "octal", where each octal digit maps directly to exactly three binary digits. But over time the standard length of a memory location settled on the "8-bit byte" and power-of-two multiples of it such as 16-, 32-, and 64-bit groups. Unless the number base chosen is an integral divisor of 8, problems arise when working with such groupings. Thus we really need to use either a Base-4, Base-16, or Base-256 number system since these represent 2-, 4-, and 8-bit groupings respectively. Base-4 is too small and has many of the same problems as Base-2. Base-256 is far too large and just dealing with that many symbols would be a challenging task. Fortunately the remaining alternative, Base-16, is close enough to Base-10 that humans can work with it quite readily.
Base-16, also known as "hexadecimal" or simply "hex", uses sixteen symbols to represent the digit values 0 through 15. The first ten of these are the same as the Base-10 symbols, for obvious reasons. The remaining six are simply the first six characters of the alphabet, A through F. To denote that a number is written in a particular base, the number base is ideally written as a subscript following the number. However, this is not something that can be done in a typical text file and so an alternate means is necessary. Two common ways have evolved over time for denoting hexadecimal numbers. The first is to place an 'H' following the number, such as 93H. The second is to preface the number with the characters '0x' such as 0x93. We will generally use the latter since this is the method used by the C programming language.
| Hex | Dec | Bin | # x 16 | # / 16 | 1's comp | Hex | Dec | Bin | # x 16 | # / 16 | 1's comp |
| 0 | 0 | 0000 | 0 | 0.0000 | F | 8 | 8 | 1000 | 128 | 0.5000 | 7 |
| 1 | 1 | 0001 | 16 | 0.0625 | E | 9 | 9 | 1001 | 144 | 0.5625 | 6 |
| 2 | 2 | 0010 | 32 | 0.1250 | D | A | 10 | 1010 | 160 | 0.6250 | 5 |
| 3 | 3 | 0011 | 48 | 0.1875 | C | B | 11 | 1011 | 176 | 0.6875 | 4 |
| 4 | 4 | 0100 | 64 | 0.2500 | B | C | 12 | 1100 | 192 | 0.7500 | 3 |
| 5 | 5 | 0101 | 80 | 0.3125 | A | D | 13 | 1101 | 208 | 0.8125 | 2 |
| 6 | 6 | 0110 | 96 | 0.3750 | 9 | E | 14 | 1110 | 224 | 0.8750 | 1 |
| 7 | 7 | 0111 | 112 | 0.4375 | 8 | F | 15 | 1111 | 240 | 0.9375 | 0 |
The table above gives the decimal and binary representations of the sixteen hexadecimal digits as well as the result when the digit is multiplied by sixteen and when it is divided by sixteen. The last column is the "one's complement" of the hexadecimal digit. The product and quotients are useful when converting between decimal and hexadecimal. The one's complement, which is simply the result of inverting each of the digits in the binary representation, is useful for taking the two's complement (i.e., the negative) of a hexadecimal number as will be shown shortly.
As humans, we are very conversant with variable width numbers. If we need five digits to represent a number, we use five digits. If we multiply two numbers together and the result is nine digits, we use nine digits. But computers don't work that way. They have a fixed number of bits (which is short for "binary digits") in a given representation, they use all of those bits to represent any number that can be represented by that representation, and they are incapable of representing values that require more bits than that. This is a major constraint that has major implications for computer programs. As it turns out, it also opens the door for a few tricks that allow us to turn these restrictions to our advantage as we shall see when we develop a means for representing negative integers.
Because the width of a given representation is so important, a whole class of terms has arisen to describe them. The most fundamental, the "bit", represents a single binary digit. As pointed out previously, the word "bit" itself is a shortened form of the phrase "binary digit". Because computer programmers are notorious for their (some would say twisted) sense of humor, a bunch of "bits" became known collectively as a "byte". Today, the overwhelming number of processors now in production are grounded in the 8-bit byte, but it is good to understand that "byte" does not necessarily mean eight bits, it is simply the primary data width for a particular processor - there are processors with 4-bit bytes, 6-bit bytes, 9-bit bytes and other widths as well.
A "nibble" (again reflecting some programmer's sense of humor) seems to be pretty universally agreed upon as being four bits, regardless of the size of the byte on a particular machine. This is probably because it requires four bits to represent all of the decimal digit values. This is also why hexadecimal is so prevalent in computer programming, even though it is more difficult to work with than octal, since a 4-bit nibble exactly corresponds to a single hexadecimal digit.
Larger width representations are almost always integer multiples of bytes for a given machine. A "word" is generally taken to mean two bytes or, for most systems, sixteen bits and a "double word" or "dword" is generally taken to mean two words, or four bytes, or thirty-two bits for most systems. A "quad word" or "qword" is four words or eight bytes which is sixty-four bits on most systems. It should be noted that these definitions are not universal. In particular, the term "word" is frequently used to refer to the width of a modern processor's data path and/or the width of the memory architecture. Historically, the term "byte" would have used for this (in the sense that the processor or memory works with data "one byte at a time"), but since "byte" has pretty firmly settled on meaning eight bits, the term "word" seems to have taken its place as having a flexible meaning. This can cause confusion, so be prepared to occasionally spend a bit (no pun intended) of time figuring out what is meant by "word" when reading technical documents.
In this course, unless specifically stated otherwise, the following widths will be associated with each of these terms:
| size | bits | bytes |
| bit | 1 | 1/8 |
| nibble | 4 | 1/2 |
| byte | 8 | 1 |
| word | 16 | 2 |
| dword | 32 | 4 |
| qword | 64 | 8 |
Different memories have different ways of physically storing a '0' or a '1', a hard disk stores it as one of two orientations of a magnetic region on the disk, a CD stores it as one of two reflective states at a region of the disk, main memory generally stores it as either a charged or a discharged capacitor, while faster memories typically store it as a high voltage or a low voltage on a specific node. What is important is that each bit can take on one of two physical states and these states are somewhat arbitrarily assigned the logical designation '0' and '1', or 'LO' and 'HI', or 'FALSE' and 'TRUE'.
On some devices a low voltage might represent a logical 'FALSE' and in another device on the same computer a low voltage might represent a logical 'TRUE'. Making sure that all of these representations interact properly is the responsibility of the hardware engineers and the operating system designers. At the level you will be working with (in this course), it is sufficient to understand that, at the level of a single bit, a '1', a 'HI' and a 'TRUE' all have the same representation as far as your programs are concerned.
Limiting the discussion to nonnegative (i.e., unsigned) integers for the moment, the most common way of representing an integer using the pattern of zeroes and ones stored in a computer's memory is using weighted binary which is simply the positional numbering system we have been referring since the beginning using Base-2.
Recall that numbers in memory have fixed widths, so if we are working with a 1-byte integer and are representing the number sixteen, it is not completely correct to say that the representation stored in memory is 10000. The actual representation is 00010000.
In many cases, ignoring the leading zeroes causes no problem, but in other cases it leads to incorrect results. It is best to include the representation of all the bits by default and only take shortcuts as a conscious decision based on an assessment of the risk of making a mistake as a consequence. As you work with the various ways values stored in memory get manipulated, you will gain the necessary insight in order to make informed assessments of this risk. Until then, play it safe and be explicit in your representations.
Thinking back to our decimal system, if asked how many values can be represented by a six-digit decimal number, the answer is one million. Note that we cannot represent the number one million itself, as this requires seven digits. But we can represent a total of one million values because one of those values is zero, and we can represent every value from zero up to but not including one million.
Expressing this in terms of the number of digits N and the base B, we can represent BN values that range from 0 to (BN - 1). For our basic widths, this means the largest value (in decimal) we can represent is:
| size | bits | largest representable value |
| bit | 1 | 1 |
| nibble | 4 | 15 |
| byte | 8 | 255 |
| word | 16 | 65,535 |
| dword | 32 | 4,294,967,295 |
| qword | 64 | 18,446,744,073,709,551,615 |
It should be noted that, while many of the newer processors are internally capable of working with 64-bit words, few programming languages yet support this. This increased ability is primarily used to optimize operations and increase data transfer speeds.
For the most part, little is lost as a result because integers greater than 32-bits are rarely needed. This is not to say that they are never needed and programming languages and extensions to languages do exist to work with arbitrarily large integers - even on machines that don't support data that wide directly. The computations are merely done in steps by software once the intrinsic limits of the processor are reached.
To show how large a 64-bit value is, consider a computer that did nothing but count starting from zero and incremented its count at 1 GHz (or 1 billion times per second) would take more than 584 years to reach the representation limit of a 64-bit value. By comparison, the 32-bit limit would be reached in less than five seconds!
If the largest value that can be represented by a 16-bit unsigned integer is 65,535 then what happens when 536 is added to 65,000? The result, 65,536, would require 17 bits to represent and therefore cannot be represented. This is known as an "overflow" condition. Likewise, subtracting a larger number from a smaller number results in an overflow because negative quantities can't be represented.
But even though the ideal result can't be represented, there is still a result and that result still represents some value. Those 16 bits still exist and each one of them still has either a '0' or a '1' stored in it. The resulting 16-bit unsigned integer still has a value. So what value is it?
Before getting into any more detail in this topic, it is important to note that we are venturing into what is known as "implementation dependent behavior" - meaning that when something like overflow occurs it is entirely possible to get different results on different computers or when using programs written in different languages. Some implementations might crash, some implementations might generate a warning flag or a warning message, and others might blindly proceed as best they can.
For those that blindly proceed, which includes most implementations of the C programming language, the result is simply the lowest 16-bits of whatever the result should have been. This means that 536 added to 65,000 is zero, because the only bit that would have been a '1' was the 17th bit.
The same is true for subtraction. If 2 is subtracted from 1, the result would be 65,535 because the normal rules for subtraction would result in borrows flowing out past the 16th bit where they become lost leaving all of the remaining sixteen bits set to a '1'.
Therefore, the integer data formats generally exhibit what is known as "wrap-around" when they overflow. Although this behavior can sometimes be useful, it is more often the cause of subtle logic errors that are difficult to track down unless the person doing the tracking is aware of and conversant with these limitations.
Now the time has come to finally tackle the issue of how to represent negative integers in a computer. We said that humans invented the "minus sign" that we tack on to the left of a negative quantity. Can we do this in a binary representation? The answer is "yes", and it is a viable way of doing it, but it is also not a particularly efficient way.
To use this method, we devote the leftmost bit as a "sign bit" and interpret the remaining bits as the unsigned (i.e., absolute value) of the number being represented. This representation is known as "signed binary" and is used from time to time. But it is not very efficient for two principle reasons. First, it requires that a lot of special rules be employed - just like the rules that we unconsciously apply when we work with signed arithmetic. Second, it requires that different algorithms be used to add two integers that have the same bit pattern depending on whether the bits represent signed or unsigned numbers.
For instance, consider the possibilities in a 3-bit system:
| pattern | unsigned | signed |
| 000 | 0 | 0 |
| 001 | 1 | 1 |
| 010 | 2 | 2 |
| 011 | 3 | 3 |
| 100 | 4 | -0 |
| 101 | 5 | -1 |
| 110 | 6 | -2 |
| 111 | 7 | -3 |
The first thing to note is that there are two representations of "zero" - basically a "positive zero" and a "negative zero". Most systems that use signed binary go to some lengths to trap occurrences of "negative zero" and convert it to the normal representation of zero.
It is instructive to note at this point that we can always expect to have at least one troublesome value when we deal with signed values (as long as we are working with an even number base, such as two). The reason is that the total number of values we can represent is even; yet if we are going to be able to represent a set of strictly positive integers, their additive inverses, and zero, we need an odd number of representations. Therefore we will always either have a value for which we cannot represent its additive inverse, or we are going to have more than one way of representing at least one value (usually zero).
Unsigned Addition Table
| + | 000 (0) | 001 (1) | 010 (2) | 011 (3) | 100 (4) | 101 (5) | 110 (6) | 111 (7) |
| 000 (0) | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| 001 (1) | 001 | 010 | 011 | 100 | 101 | 110 | 111 | [000] |
| 010 (2) | 010 | 011 | 100 | 101 | 110 | 111 | [000] | [001] |
| 011 (3) | 011 | 100 | 101 | 110 | 111 | [000] | [001] | [010] |
| 100 (4) | 100 | 101 | 110 | 111 | [000] | [001] | [010] | [011] |
| 101 (5) | 101 | 110 | 111 | [000] | [001] | [010] | [011] | [100] |
| 110 (6) | 110 | 111 | [000] | [001] | [010] | [011] | [100] | [101] |
| 111 (7) | 111 | [000] | [001] | [010] | [011] | [100] | [101] | [110] |
Signed Addition Table (using signed-binary representation of negative numbers)
| + | 000 (0) | 001 (1) | 010 (2) | 011 (3) | 100 (-0) | 101 (-1) | 110 (-2) | 111 (-3) |
| 000 (0) | 000 | 001 | 010 | 011 | 000 | 101 | 110 | 111 |
| 001 (1) | 001 | 010 | 011 | [100] | 001 | 000 | 101 | 110 |
| 010 (2) | 010 | 011 | [100] | [101] | 010 | 001 | 000 | 101 |
| 011 (3) | 011 | [100] | [101] | [110] | 011 | 010 | 001 | 000 |
| 100 (-0) | 000 | 001 | 010 | 011 | 000 | 011 | 110 | 111 |
| 101 (-1) | 101 | 000 | 001 | 010 | 101 | 110 | 111 | [000] |
| 110 (-2) | 110 | 101 | 000 | 001 | 110 | 111 | [000] | [001] |
| 111 (-3) | 111 | 110 | 101 | 000 | 111 | [000] | [001] | [010] |
Where overflow occurs, remember that the result is implementation dependent and therefore the values in the above table are only one possible result. The combinations above that are in shaded boxes represent combinations that resulted in some kind of overflow. These combinations are also surrounded by square brackets in case the shading does not show up on your display device. The remaining boxes, however, represent combinations that did not result in any kind of overflow and therefore must yield the results shown.
Note that, given the same pattern of 0's and 1's as arguments, say adding 101 to 001, the result is a very different pattern of 0's and 1's depending on whether the arguments represent signed (result is 000) or unsigned (result is 110) integers. This means that the actual hardware that adds signed integers must be different from the hardware that adds unsigned integers. It turns out that the hardware to do unsigned addition is very simple while the hardware to do signed addition on signed-binary numbers is considerably more complicated - because of all the special rules mentioned previously.
Another way of representing negative numbers using binary integers is to simply shift the values by a fixed amount. If we consider the unsigned representation, we note that the values represented go from the minimum to the maximum as the binary values go from all zeroes to all ones. What if we simply shift the representations by subtracting four from each unsigned value but keep the order the same?
| pattern | unsigned | signed |
| 000 | 0 | -4 |
| 001 | 1 | -3 |
| 010 | 2 | -2 |
| 011 | 3 | -1 |
| 100 | 4 | 0 |
| 101 | 5 | 1 |
| 110 | 6 | 2 |
| 111 | 7 | 3 |
The amount of the offset is known as the "excess", so the above table represents and Excess-4 representation. Notice that we still preserve the concept of a "sign bit" - it just happens to be inverted from our prior representation. If we prepare the addition table for this representation, we get:
Unsigned Addition Table (same table as before)
| + | 000 (0) | 001 (1) | 010 (2) | 011 (3) | 100 (4) | 101 (5) | 110 (6) | 111 (7) |
| 000 (0) | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| 001 (1) | 001 | 010 | 011 | 100 | 101 | 110 | 111 | [000] |
| 010 (2) | 010 | 011 | 100 | 101 | 110 | 111 | [000] | [001] |
| 011 (3) | 011 | 100 | 101 | 110 | 111 | [000] | [001] | [010] |
| 100 (4) | 100 | 101 | 110 | 111 | [000] | [001] | [010] | [011] |
| 101 (5) | 101 | 110 | 111 | [000] | [001] | [010] | [011] | [100] |
| 110 (6) | 110 | 111 | [000] | [001] | [010] | [011] | [100] | [101] |
| 111 (7) | 111 | [000] | [001] | [010] | [011] | [100] | [101] | [110] |
Signed Addition Table (using offset binary representation of negative numbers)
| + | 000 (-4) | 001 (-3) | 010 (-2) | 011 (-1) | 100 (0) | 101 (1) | 110 (2) | 111 (3) |
| 000 (-4) | [100] | [101] | [110] | [111] | 000 | 001 | 010 | 011 |
| 001 (-3) | [101] | [110] | [111] | 000 | 001 | 010 | 011 | 100 |
| 010 (-2) | [110] | [111] | 000 | 001 | 010 | 011 | 100 | 101 |
| 011 (-1) | [111] | 000 | 001 | 010 | 011 | 100 | 101 | 110 |
| 100 (0) | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| 101 (1) | 001 | 010 | 011 | 100 | 101 | 110 | 111 | [000] |
| 110 (2) | 010 | 011 | 100 | 101 | 110 | 111 | [000] | [001] |
| 111 (3) | 011 | 100 | 101 | 110 | 111 | [000] | [001] | [010] |
Although the pattern of 0's and 1's is different in the two tables, there is a very simple mapping between them - the most significant bit (sign bit) is inverted and everything else is the same. This means that it is possible to take the hardware adder that works for unsigned integers and, with only a simple modification, make it work for both signed and unsigned integers, although it still must be told which representation is being used.
The principal drawback of offset binary is that, for numbers that exist in both the signed and the unsigned representations, the representations are different. It would be convenient if this were not the case.
In the days of mechanical adding machines (most of which worked directly in base-10), a quick and simple way of representing a negative integer was found in using the lower half of the range for positive numbers and the upper half of the range represented negative numbers with the representation of a particular negative number being obtained by subtracting the absolute value of it from the largest representable pattern, which was a pattern of all 9s. This was mechanically simple because taking the negative of a number involved only subtracting each digit from 9, which was guaranteed not to produce any borrows. In base-10, this is known as "9's complement". In general, in base-B this technique is known as "(B-1)'s complement" where B is the number base, also known as the radix. Since the representation uses the number radix reduced (diminished) by 1, this representation is generically referred to as "diminished radix complement".
Mathematically, the "N-digit diminished radix-B complement" can be defined as follows:
(-A) = (BN-1) - A
In the case of binary, the diminished radix complement is known as "1's complement" and involves subtracting the absolute value from a pattern of all ones. As with any diminished radix complement negation, no borrows result. But it is also the case that subtracting a 0 from a 1 yields a 1, while subtracting a 1 from a 1 yields a 0. In other words, the result is simply the bitwise negation of the value being negated. The bitwise negation is frequently indicated using the tilde (~) symbol, so ~A is simply A with each bit flipped.
Therefore, 1's complement is a special case in which
(-A) = (BN-1) - A => ~A (for the case of base-2)
While it is very simple to implement negation in 1's complement, using an unsigned adder to perform arithmetic has difficulties. As just one example, adding a number and its additive inverse does not yield zero, or, more explicitly, it doesn't yield a pattern of all zeros. Instead, it yields a pattern of all ones. But, arguably, this is zero since if you take the additive inverse of 0 you get a pattern of all ones. Thus, there are two ways of representing zero, which is problematic. Related to this, adding a positive and a negative value will result in a value that is one smaller than it should be. For instance, using a 4-bit representation, -3 is represented by 1100 while +5 is represented by 0101. Adding these with an unsigned adder yields the pattern 0001 (+1) instead of the correct answer of 0010 (+2). Because this only manifests itself when a positive and a negative value are added together, it is fairly straightforward to modify a conventional unsigned adder to yield the correct results when working with 1's complement values, but it must be aware of when it is and when it is not working with such values.
It would be very convenient if we could devise a representation where our hardware adder didn't have to distinguish between signed and unsigned integers. We can accomplish this as long each non-overflowing sum has the same pattern of 0's and 1's regardless of whether the input pattern is for a signed or an unsigned integer. The difference would come at the end when it came time to interpret what value the resulting pattern of 0's and 1's represented.
To devise this representation, we draw upon two properties that we have discussed previously. First, the negative of a number is defined as being the additive inverse, meaning that the addition of a number and its negative yields a result of zero. The second property is the overflow property of fixed-width integers whereby if the result of an addition operation yields 2N, where N is the number of bits, then normal overflow behavior will wrap around and yield a result of zero.
Combining these two properties, we can then define the negative of a number, for a fixed width representation, as follows;
Given a number A, the number (-A) is the negative of A if the following is true:
A + (-A) = 0 (always true)
A + (-A) = 2N
since, for an N-bit representation, 2N is equivalent to zero.
Hence,
(-A) = 2N - A
It is important to note that this result is not the general representation for the negative of A, which is given by the original expression of A+(-A)=0. So the pattern that results from using this expression is a specific representation of (-A) known as the "N-bit 2's complement of A".
This same procedure can be applied to any number base. In general, for an N-digit representation in any positive integral number base BN is equivalent to zero, and hence we can define
(-A) = BN - A
For instance, if base-10 is being used with 4-digit numbers, then if we represented negative values using "4-digit 10's complement", we would represent -1234 using the pattern 8766.
This representation is known as "radix complement". The term "radix" simply refers to the number base.
It should be noted that the term "N-digit R's complement" is actually ambiguous; For instance, is 7's complement referring to a base-7 system (radix complement) or a base-8 system (diminished radix complement)? So a technically correct description would be something like "N-digit radix-B complement". However, saying "16-bit 2's complement" is unambiguous because "bit" is short for "binary digit" and, hence, using "bit" implies a radix of two.
It is a simple matter to build up a table of the 2's complements for all of the values in our N-bit number system. For our three-bit system it yields:
| pattern | 3-bit 2's complement |
| 000 | 000 |
| 001 | 111 |
| 010 | 110 |
| 011 | 101 |
| 100 | 100 |
| 101 | 011 |
| 110 | 010 |
| 111 | 001 |
In building up this table, we could do the math in either decimal or binary - both are about the same difficulty.
Example: Find the 3-bit 2's complement of 3.
Solution:
A = 3
(-A) = 23 - 3 = 8 - 3 = 5
(-A) = 1012
Or:
A = 3 = 0112
(-A) = 2N - 0112 = 10002 - 0112
(-A) = 1012
Note that, with one exception, the 2's complements are unique in that a given nonzero pattern has exactly one 2's complement and that the 2's complements appear in pairs: 011 is the 2's complement of 101 and 101 is the 2's complement of 011. This is the behavior that we expect from numbers and their additive inverses.
The next step is to decide which of the two complementary values is positive and which is negative. While technically an arbitrary choice, there is really only one reasonable choice. There is no reason to have the representation for a positive number in an unsigned system be different than the representation for that same positive number in an unsigned system if it is easily avoidable. Therefore the number in each pair that has a leading zero is considered the positive member of the pair and is interpreted according to the normal rules for unsigned integers.
| pattern | decimal | 2's comp | negative |
| 011 | 3 | 101 | -3 |
| 010 | 2 | 110 | -2 |
| 001 | 1 | 111 | -1 |
| 000 | 0 | 000 | 0 |
| 111 | -1 | 001 | 1 |
| 110 | -2 | 010 | 2 |
| 101 | -3 | 011 | 3 |
| 100 | ? | 100 | ? |
Examination of the above table yields the useful property that, as with signed-binary, the leftmost bit (also known as the "leading" bit) serves as a "sign bit" with positive values having a leading '0' and negative values having a leading '1'.
As with the signed-binary representation, we have one value that can cause us problems. The pattern 100 (or, in general, the N-bit pattern consisting of all 0's except a leading '1') can either be interpreted as -4 (in the 3-bit case) based on it being the result of (-3) - (1) or it can be interpreted as being an alternate representation for zero based on the fact that it is its own 2's complement and, normally, only zero can be its own additive inverse. Almost all implementations treat it as the most negative number representable because this is the behavior exhibited when most operations that are carried out on it. The operations for which it is ill-behaved are then considered to be situations in which overflow has occurred and hence the pattern that results from the operation has no particular meaning. Consider the case of when you take its negative, for instance. The negative of -4 should be +4, but we can't represent +4 in our system and so overflow had to have taken place. Although the resulting pattern doesn't have to have any particular property, it is interesting to note that we get the same pattern from trying to take the negative of -4 as we get if we try to add 1 to 3.
The utility of the two's complement representation starts to become apparent when you examine the above table more closely. Notice that if the unsigned values 111 and 001 are added together, normal overflow yields a result of 000 which is the correct result for adding the signed integers 111 and 001 (if the two's complement representation is used). The same is true for all of the other values and can be summed up by the observation that the normal wraparound behavior for unsigned integers results in the correct translations between the positive and negative regions for signed integers using the two's complement representation. This is a powerful statement because it means that hardware that can handle addition and subtraction for unsigned integers can automatically handle addition and subtraction for signed integers if they use the two's complement representation. The same is not true for other operations, but addition is by far one of the most fundamental and frequently used operations in a processor - in fact many processors do not support multiplication or division at all.
Another useful artifact of the two's complement notation is that if we are comparing two signed integers to see which is larger (with any positive number being larger than any negative number) we see that we can first compare the most significant bit. If they are different, then we need go no further and the value that starts with a '1' is larger if the representations are unsigned, and the value that starts with a '0' is larger if the representations are signed. If the most significant bits are the same, then we can compare the remaining bits as simple unsigned integers without regard to whether they represent a signed, unsigned, positive, or negative value. We don't even have to make the effort to exclude the most significant bit from the comparison because, since they are the same in this case, they have no impact on the outcome.
Unsigned Addition Table (same table as before)
| + | 000 (0) | 001 (1) | 010 (2) | 011 (3) | 100 (4) | 101 (5) | 110 (6) | 111 (7) |
| 000 (0) | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| 001 (1) | 001 | 010 | 011 | 100 | 101 | 110 | 111 | [000] |
| 010 (2) | 010 | 011 | 100 | 101 | 110 | 111 | [000] | [001] |
| 011 (3) | 011 | 100 | 101 | 110 | 111 | [000] | [001] | [010] |
| 100 (4) | 100 | 101 | 110 | 111 | [000] | [001] | [010] | [011] |
| 101 (5) | 101 | 110 | 111 | [000] | [001] | [010] | [011] | [100] |
| 110 (6) | 110 | 111 | [000] | [001] | [010] | [011] | [100] | [101] |
| 111 (7) | 111 | [000] | [001] | [010] | [011] | [100] | [101] | [110] |
Signed Addition Table (using two's complement representation of negative numbers)
| + | 000 (0) | 001 (1) | 010 (2) | 011 (3) | 100 (-4) | 101 (-3) | 110 (-2) | 111 (-1) |
| 000 (0) | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| 001 (1) | 001 | 010 | 011 | [100] | 101 | 110 | 111 | 000 |
| 010 (2) | 010 | 011 | [100] | [101] | 110 | 111 | 000 | 001 |
| 011 (3) | 011 | [100] | [101] | [110] | 111 | 000 | 001 | 010 |
| 100 (-4) | 100 | 101 | 110 | 111 | [000] | [001] | [010] | [011] |
| 101 (-3) | 101 | 110 | 111 | 000 | [001] | [010] | [011] | 100 |
| 110 (-2) | 110 | 111 | 000 | 001 | [010] | [011] | 100 | 101 |
| 111 (-1) | 111 | 000 | 001 | 010 | [011] | 100 | 101 | 110 |
Notice that the patterns of 0's and 1's in both tables are identical. This means that we have achieved the goal of being able to use the same hardware to carry out addition of both unsigned integers and signed integers that use the two's complement format.
It turns out that determining whether overflow has occurred, while depending on whether the arguments and results are interpreted as signed or unsigned, is also very straightforward in either case and can be carried out by looking only at the leading bits of both arguments and the result.
Overflow results for C = A + B
(leading bit of A, B, and C)
| A | B | C | unsigned | signed |
| 0 | 0 | 0 | no | no |
| 0 | 0 | 1 | no | yes |
| 0 | 1 | 0 | yes | no |
| 0 | 1 | 1 | no | no |
| 1 | 0 | 0 | yes | no |
| 1 | 0 | 1 | no | no |
| 1 | 1 | 0 | yes | yes |
| 1 | 1 | 1 | no | no |
The pattern 100 is still not well behaved but notice that the overflow test does work as long as this pattern is interpreted at -4.
If asked to determine the two's complement representation of a number, you must first know what the width of the representation is. Remember, the trick that we used to develop this representation relied on the overflow behavior that occurs because of the finite width available to store a value.
Let's say that we are asked to compute the 8-bit two's complement representation for -73. We can do this a couple of different ways. We could do this by using our definition and saying that the representation is the same as that for the 8-bit unsigned value for (256-73)
256 - 73 = 183
Convert 183 to hex with the aid of our Hexadecimal Reference Table
183 / 16 = 11.4375 The 0.4375 means a digit of '7'
11 / 16 = 0.6875 The 0.6875 means a digit of '11' or 'B'
The zero whole number part means we are done. Of course, in practice, as soon as the whole number part drops below the size of the base (sixteen in our case) there is no need to actually perform the last division - it was done above just to conform to the given algorithm.
So our 8-bit binary representation for -73 is
-73 = 0xB7 = 1011 0111
Few people actually compute it this way because, frankly, few people understand that this is the defining condition for the two's complement format. Instead, they have been shown a technique that works even though they probably have no idea of why it works. You will.
Consider our defining condition again:
A + (-A) = 2N
(-A) = 2N - A
Note that 2N is NOT an N-bit number. But what if we write it as
2N = (2N-1) + 1
So now we have
(-A) = (2N-1) + 1 - A = [(2N-1) - A] + 1
The representation for (2N-1) is an N-bit number consisting of all 1's. Just as is the case if we subtract a decimal number from an equal length decimal number consisting of all 9's, we are guaranteed to generate no borrow operations. So we can treat each digit one at a time. If we subtract a '0' from '1' we get '1' whereas if we subtract '1' from '1' we get zero. Hence the result is the same as that achieved by simply inverting each bit (changing each '1' to a '0' and vice versa) in the number being subtracted. We'll represent this "bitwise inversion" operation with the tilde character '~'. This means that:
[(2N-1) - A] = ~A
leaving us with the result
(-A) = ~A + 1
This is the formula that most people blindly follow. They couldn't tell you where it comes from or why it works. Furthermore, most people have a hard time remembering whether you invert the bits and then add a one, or if you add a one and then invert the bits. You should never have this problem because you know where the formula comes from and can re-derive it from scratch if need be. That's the difference between comprehending something and simply memorizing it.
So let's see how we use this formula since it is quite useful when we are starting out with a representation that is already in binary or, as we shall see, in hexadecimal. Using the definition directly is more useful when we work in decimal initially, as we did above.
First, if we are going to determine ~A, we must first express A in binary.
A = 73
73 / 16 = 4.5625 => A = 0x49 => 0100 1001
~A = 1011 0110
(-A) = ~A + 1 = 1011 0111 = 0xB7
The subtraction of a number from a pattern consisting of all 1's is called the "one's complement" of the number. Notice that the 1's complement is included in our Hexadecimal Reference Table so that we can avoid going all the way to binary:
A = 73
73 / 16 = 4.5625 => A = 0x49
~A = 0xB6
(-A) = ~A + 1 = 0xB6 + 0x01= 0xB7
Aside: To avoid confusion, recognize that you can't think of the "one's complement" and "two's complement" as being the same thing except with a different number or a different base. In base B, the complements are:
N-digit B's complement of A in Base B is BN - A
N-digit (B-1)'s complement of A in Base B is (BN - 1) - A
For any given base this method of representing negative integers is valid. So for base-10, we can represent negative values using the ten's complement. Mechanical computing devices commonly did this before the advent of electronic calculators. We can compute the ten's complement very easily by first taking the nine's complement and adding one. But we could also work in base-9 where we would also have a nine's complement. However, the base-9 nine's complement and the base-10 nine's complement are fundamentally different concepts.
From a purist's perspective, our normal integer representations are simply a special case of a fixed point representation where the radix happens to be located just to the right of the rightmost digit. While true, the almost universal use when someone talks about using a "fixed point" representation is when the programmer uses an integer representation but chooses to interpret the results as though the radix point existed at some location other than after the rightmost digit. Usually they the effective radix point location moved to the left so that they can work with fractional values but it is equally valid to move the radix point to the right so that they can work with larger values than they would have otherwise been able to represent.
Generic fixed point representations are seldom an explicit choice supported by a processor's instruction set. As a result, the use of fixed-point arithmetic almost always involves a software implementation of the representation along with all of the manipulation rules.
On today's modern processors and for the majority of applications, the use of fixed point arithmetic is seldom justified given the adequacy of simply using the intrinsic floating point support that is available. But when working with high precision applications, applications where speed and performance are essential, or when working with the slower, less sophisticated processors found in embedded systems the use of fixed-point arithmetic is very common.
One advantage of fixed-point arithmetic is that it permits working with fractional values even on machines that only support integer operations. Another advantage comes from the fact that, on most machines that support both integer and floating point computations, integer operations are much faster and generally more precise than equivalent floating point counterparts.
The primary disadvantage is that the programmer is responsible for the overhead of determining both the representation and implementing the software needed to manipulate values that use that representation - although having this level of control opens the door for the programmer to further optimize the algorithms to attain better performance. Another limitation is that the range of values that can be represented falls well short of that available to comparable floating point representations.
For an example, let's say that we want to use a decimal-based fixed point representation to do our accounting. We want to achieve the following goals: (1) be able to work with any quantity of money less than one million dollars; (2) be able to report quantities to the nearest penny; and (3) minimize the impact of accumulated round-off errors tracking quantities to the nearest 1/100 of a penny in calculations.
On paper, we would normally just be sure to track all quantities to at least four decimal places in order to give us the 1/100 of a penny requested by specification (3) above. But here we are using a fixed-point representation using integers, so we do the following:
We need to work with integers having at least ten digits - six to represent the whole dollar amounts from $0 through $999,999; two more to represent the number of cents; and a final two to represent the number of hundredths of a cent. So the quantity $50,264.81 would be represented as the integer 0502648100.
Some of the rules that need to be observed when manipulating values stored in this representation include:
Switching over to an 8-bit unsigned binary fixed point representation, let's discuss how to convert decimal numbers to the fixed point representation and back. Our representation will place the radix point after the second bit:
| b7 | b6 | (rp) | b5 | b4 | b3 | b2 | b1 | b0 |
| M3 | M2 | . | M1 | M0 | E3 | E2 | E1 | E0 |
Note: Only the bits labeled bn are actually stored.
The direct interpretation of the bits stored under this representation means that the value represented is given by:
v = (b7 x 21)+(b6 x 20)+(b5 x 2-1)+(b4 x 2-2)+(b3 x 2-3)+(b2 x 2-4)+(b1 x 2-5)+(b0 x 2-6)
Using this relationship, let's represent the quantity π as best we can using this representation:
π ~= 3.14159
r = 3.14159265 (r is the remainder)
To get b7 : is r > 21? (21 = 2)
Yes: b7 = 1 and r = r - 21 = 1.14159265
To get b6 : is r > 20? (20 = 1)
Yes: b6 = 1 and r = r - 20 = 0.14159265
To get b5 : is r > 2-1? (2-1 = 0.5)
No: b5 = 0
To get b4 : is r > 2-2? (2-2 = 0.25)
No: b4 = 0
To get b3 : is r > 2-3? (2-3 = 0.125)
Yes: b3 = 1 and r = r - 21 = 0.01659265
To get b2 : is r > 2-4? (2-4 = 0.0625)
No: b2 = 0
To get b1 : is r > 2-5? (2-5 = 0.03125)
No: b1 = 0
To get b0 : is r > 2-6? (2-6 = 0.015625)
Yes: b0 = 1 and r = r - 21 = 0.00096765
The next bit would be a 0, so we don't need to round up, hence our fixed point binary representation for π is 1100 1001 which represents 11.0010012.
We can certainly work with this expression and do what we need to do, working with negative powers and the consequent division operations and/or multiplication by fractional values is time consuming and error prone. The above example should make you cry out for a better way.
Plus, we have already seen that we can be much more efficient if we can perform much of our work in hexadecimal converting back and forth to binary only when necessary. But the above representation, as given, does not appear to lend itself to working with hexadecimal because the nibble boundaries do not match hexadecimal digit boundaries.
But what happens if I multiply a quantity by a constant and then divide it by that same constant? As long as the constant is not zero, I have not changed anything at all. Considering a decimal example, I can write:
3.14159 = (3.14159 x 10000) / 10000 = 31459 / 10000
Notice that the quantities in the right most expression are all integers and the division operation can be carried out by simply shifting the decimal point four places to the left.
The exact same property applies to binary values:
π = 11.0010012 = (11.0010012 * 26 ) / 26 = 110010012 / 26
Looking at the rightmost expression, we see an integer divided by the base raised to the sixth power, which is the same as moving the radix point six places to the left. But this is precisely where we want the radix point to be in our representation.
So the bit pattern in the integer 110010012 is the bit pattern we need to store. If we didn't already know this bit pattern, we could easily get it by using the following steps:
π = X / 26
X = 26 * π = 64π = 201.1
Since we want only the integer X, we round 201.1 to the nearest integer and convert it to binary:
201 / 16 = 12.5625 => (0x12).(0x9) => 0xC9 = 1100 1001 2
Hopefully you will agree that this is a much faster, easier, and less error prone method.
The same method can be used to convert a fixed point binary value back to decimal.
What is the decimal value represented by the binary value 1010 1110 under the fixed point system we have been using - namely six bits to the right of the binary point?
With six bits to the right of the binary point, the value represented is the integer value divided by 26 or:
v = 1010 11102 / 26
v = 0xAE / 64 = ((10*16)+14 ) / 64 = 174 / 64 = 2.71875
The representation of floating point values is not particularly straightforward as it embodies some rather interesting properties. But once those properties are understood, the peculiarities of the representation become quite understandable.
First, let's start with a basic floating point representation and explore its deficiencies. Then we will move toward the accepted representation as a result of addressing these deficiencies.
Recall that a floating point value consists of two parts - the mantissa and the exponent. If our representation is to fit into a fixed number of bits - which it must do - then we must decide how many bits to use for the mantissa and how many bits to use for the exponent.
As with most things in engineering, this decision involves a compromise. To understand this compromise and make it in an informed way, we need to understand the properties that are being traded off against each other. In the case of the mantissa and the exponent, we are trading static range for dynamic range. The more bits we allocated to the mantissa, the better the static range, but it is achieved at the expense of the dynamic range. Conversely, we can improve dynamic range by increasing the number of bits used for the exponent if we are willing to accept a poorer level of static range. The only alternative is to increase the total number of bits used in the overall representation.
For the purposes of our discussions below on static and dynamic range, let's use the decimal system and stipulate that the mantissa can consist of at most six digits, while the exponent can exist of at most two digits.
The "static range" of a system is the ratio of the largest value that can be represented to the smallest value that can be represented.
Using our example system, the largest value we could represent would be
9.99999 x 1099
while the smallest would be
0.00001 x 10-99
The static range is therefore:
999999 x 10198 = 10204
While the static range of the system is a useful quantity, it doesn't tell us everything. In particular, we certainly can't represent a change in a value to anything approaching the static range of the system.
For instance, in the above system we can represent both the size of the U.S. Public Debt (something on the order of six trillion dollars), and the value of a penny very nicely. But we can't represent a change in the Public Debt of only a penny. In fact, the smallest change in the Public Debt that I could represent is ten million dollars!
So I need another measure that tells me the accuracy of my representation. This is tightly related to the concept of "significant figures" that most people learned about in their early chemistry and physics courses. The basic measure of accuracy is to ask how close can two numbers be to each other and still be represented as different values? The dynamic range will therefore be defined as the ratio of a number to the smallest change that can be represented in that number.
Using our example system, I could look at the difference between 1.00000 and 1.00001 or the difference between 9.99999 and 9.99998. In either case, the amount by which they differ would be 0.00001. But the calculated dynamic range would vary by a factor of ten depending on which pair of values I chose to use. If I use the first pair I would claim a dynamic range of essentially 100,000, or five digits (105). But if I use the latter pair I could claim a dynamic range of 1,000,000 or six digits.
A marketing representative would almost certainly elect to use the larger value because it allows them to claim a higher level of accuracy even though, under practical conditions, the actual accuracy attainable is always less. But engineers generally prefer to use the smaller value because then the resulting claimed accuracy is a minimum level that is always achieved. Using this as a guideline, the commonly accepted way to expressing dynamic range in a floating point value is to express the smallest value, typically called epsilon, such that 1 and 1+epsilon are two distinct values. So in our example system epsilon would be 0.00001 or five digits of dynamic range.
Now that we understand the concepts of static and dynamic range, we can start building our floating point representation. For simplicity sake, we will work with a one byte floating point number and we will allocate one nibble for the mantissa and one nibble for the exponent.
The first thing we must decide is where the radix point in the mantissa is located. We can choose it to be anywhere, but we must then be consistent with that choice. For starters, let's place the radix point at the right of the mantissa and see what the implications are. We can always change it later.
Our first inclination is probably to have both the mantissa and the exponent be two's complement signed values, since we have seen the advantages of the two's complement representation when used with integers.
Floating Point Representation #1
| b7 | b6 | b5 | b4 | (rp) | b3 | b2 | b1 | b0 |
| M3 | M2 | M1 | M0 | . | E3 | E2 | E1 | E0 |
Note: Only the bits labeled bn are actually stored.
Mantissa (m): four-bit signed integer (M3:M0)
Exponent (e): four-bit signed integer (E3:E0)
Value = m x 2e
It is instructive to fill in some of the resulting values in our table:
| pattern | value |
| 0100 1111 | 4 x 2-1 = 2 |
| 0100 1110 | 4 x 2-2 = 1 |
| 0011 1111 | 3 x 2-1 = 1.5 |
| 0011 1110 | 3 x 2-2 = 0.75 |
| 0010 1111 | 2 x 2-1 = 1 |
| 0010 0000 | 2 x 20 = 2 |
| 0001 0001 | 1 x 21 = 2 |
| 0001 0000 | 1 x 20 = 1 |
| 0000 0000 | 0 x 20 = 0 |
| 1101 1111 | -3 x 2-1 = -1.5 |
| 1010 1110 | -6 x 2-2 = -1.5 |
Using this convention, we immediately run into a very serious problem - namely one of uniqueness. With signed integers, there was one troublesome value that stemmed from the fact that we couldn't represent the same number of strictly positive values as we could strictly negative values. We dealt with it by simply expecting trouble unless we avoided the use of that troublesome value. Here the problem is much more severe in that there are numerous ways to represent the same value - for instance we can represent the value 1 three different ways.
Another serious problem is one of ordering. The entries in the above table are ordered according to the bit pattern, yet the values they represent bounce all around. This behavior, while not as fundamentally critical as the uniqueness problem, means that doing magnitude comparisons on floating point values will be a nightmare.
In short, this choice of representation is wholly inadequate, but by making a decision to try this representation and then looking at its ramifications we have identified two shortcomings which we now add to the list of features that we would like our final representation to possess: First, that no two patterns in the domain of the representation map to the same value. Second, that the ordering of the patterns in the domain have a simple relationship to the ordering of the values those patterns represent. Furthermore, since our initial representation lacks these two features, if we can identify the reasons why it lacks them we are well on the road to finding ways to modify the representation so that it possesses them.
The problem of uniqueness arises because our representation is not normalized. The term "normalized" means different things in different contexts, but generally it means mapping the values in a set to a preferred range or, in our case, representation. By normalizing the mantissa so that there is exactly one non-zero digit to the left of the radix point we eliminate most (if not all) duplicate representations.
The first thing we have to note is that the binary point is no longer to the right of the last bit in the mantissa. Instead, it is going to be located to the right of the second bit in the mantissa - the first bit is the sign bit and the second bit is the first bit in the magnitude. In our case that means that we have two remaining bits to the right of the binary point. Recall from the discussion on fixed-point numbers that we can think of this conveniently as being a four-bit integer divided by four (22). Don't forget that we need to adjust the exponents accordingly by adding two to all of them.
Floating Point Representation #2
| b7 | b6 | (rp) | b5 | b4 | b3 | b2 | b1 | b0 |
| M3 | M2 | . | M1 | M0 | E3 | E2 | E1 | E0 |
Note: Only the bits labeled bn are actually stored.
Mantissa (m): four-bit signed integer (M3:M0) divided by 22
Exponent (e): four-bit signed integer (E3:E0)
Value = m x 2e
So how do we normalize a two's complement signed integer?
If the number is positive it is very straight forward. We simply multiply the mantissa by the base, and reduce exponent by one (which is the same as dividing the value by the base), until the next-to-leftmost digit in the mantissa is a one (remember, the right most digit is the sign bit and needs to remain zero if the number is positive). Just as when multiplying a decimal value by ten, you multiply a binary value by two by shifting the bits one place to the left.
Example:
Problem: A value is represented, according to our first attempt's format, as 0010 0000. Find the normalized representation for it
Solution: Looking in the table from the last section we see that this is one of the representations for the value '2'. The first thing we need to do is make the adjustment for the location of the binary point. This is done simply by adding two to the exponent giving us 0010 0010.
The mantissa is 0010 and we can normalize this by multiplying by two giving us 0100 and decreasing the exponent by one making it 0001.
The result is 0100 0001
Check: According to our new format, the value represented by this pattern is:
value = (0100b)/4 x 2(0001b) = 4/4 x 21 = 2
If the number is negative things are just as straight forward, but not quite as obvious. Consider how we knew when to stop multiplying by two in the case of a positive value. While it was convenient to say that we stopped as soon as the next-to-leftmost bit was a '1', what we really did was stop as soon as any further multiplications by two would result in an overflow - which is signaled by the corruption of the sign bit. If we apply this same approach to negative values we have a rule similar to that for positive values - namely that we multiply by two until the next-to-leftmost bit becomes a zero.
Example:
Problem: A value is represented, according to our first attempt's format, as 1101 1111. Find the normalized representation for it
Solution: Looking in the table from the last section we see that this is one of the representations for the value '-1.5'. The first thing we need to do is make the adjustment for the location of the binary point. This is done simply by adding two to the exponent giving us 1101 0001.
The mantissa is 1101 and we can normalize this by multiplying by two giving us 1010 and decreasing the exponent by one making it 0000.
The result is 1010 0000
Check: According to our new format, the value represented by this pattern is:
value = (1010b)/4 x 2(0000b) = -6/4 x 20 = -1.5
So what are the deficiencies that this version of our floating point representation has?
First, one of our eight bits, b6, is forced to always be equal to '1' when the value is positive and '0' when the value is negative because of the normalization constraint. If it is not, we are right back were we started where we had many values that had multiple ways to represent them. So we need to limit our values and, in the process, we cut in half the number of distinct values that we can represent!
Second, while this representation has addressed the uniqueness problem, it has not addressed the ordering problem at all.
Third, we now have no way to represent zero. The fix for this problem is best left until after we have addressed the ordering problem.
Fourth, we have made it quite difficult to negate a value because we can't simply take the two's complement of the mantissa. The reason is that the result may not be properly normalized requiring us to renormalize it.
The problem of ordering arises because we placed the mantissa to the left of the exponent even though the exponent exerts, by far, a more dominant influence on the magnitude of the value being represented than does the mantissa - with the exception of the sign bit. The sign of a number is the most dominant influence. If the signs of two numbers are different then the positive number is always larger than the negative number (where size means which value lies further to the right on a normal number line such that 0.01 is larger than -100).
To make our representation reflect this, we are going to split the sign bit off from the rest of the mantissa and place it as the leftmost bit. We'll place the exponent in the next bits, and the remainder of the mantissa will be stored in the rightmost bits. Having the bits in our mantissa distributed across our bit pattern could be annoying (at least for a human working with the representation) but it is not a major problem for the hardware designer.
Another problem we have is keeping track of whether our units bit needs to be a '1' or a '0' since this depends on the sign. We can get around this problem by using a signed binary representation - and in doing so we complete the separation of the sign bit from the mantissa because now the sign bit has no affect on the magnitude of the mantissa. Our resulting three-bit mantissa is always positive and therefore always has to be normalized to have a leading '1'. A further advantage of using signed binary for the mantissa is that the difficulty we identified with negating a floating point value disappears - we simply negate the sign bit and we are done.
This hasn't eliminated the problem of what we do if the leading bit in the mantissa happens to be a '0' or the fact that we have cut the number of values we can represent in half - but there is a rather clever way around both of these problems. We simply assume that there is a '1' to the left of the binary point and don't even record it as part of the eight bits that get stored. As a result we get to record an additional mantissa bit from the right side of the binary point. Before getting too excited about this apparent "something for nothing" it should be pointed out that we have not increased the total number of values that we can represent - there are still only 2N of them. Be sure not to forget the assumed '1' that exists to the left the binary point when working directly with the representations of floating point values.
Coming back to the ordering concern, we see that if the exponent is represented in a two's complement fashion that we must treat both of the first two bits (the two leftmost bits) as special cases in our magnitude comparison since both S (b7) and E3 (b6) are sign bits. But what if the exponents were ordered so that all zeroes represented the smallest (most negative) exponent and all ones represented the largest (most positive) exponent? Now the same comparison operation used for signed integers would work for floating point values - at least as far as the sign bit and the exponent are concerned.
This leads us to use an offset binary representation for the exponent. If we use the most common convention for offset binary, then zero is represented by a leading '1' and the rest of the bits are '0's. Hence to find out the actual exponent, we would first read the exponent bits as a four bit unsigned integer and then subtract eight (1000b). Since the range of a four bit unsigned integer is from zero to fifteen, the range of our exponent becomes negative eight to positive seven.
Floating Point Representation #3
| b7 | b6 | b5 | b4 | b3 | M3 | (rp) | b2 | b1 | b0 |
| S | E3 | E2 | E1 | E0 | 1 | . | M2 | M1 | M0 |
Note: Only the bits labeled bn are actually stored.
Sign Bit (s): S
Mantissa (m): 1 + [three-bit signed integer (M2:M0) divided by 23]
Exponent (e): four-bit offset binary integer (E3:E0) - 1000b
Value = (-1)s x m x 2e
Example:
Problem: What value is represented by 0000 0000?
Solution: Grouping the bits into their logical groupings, we have (0)(0000)(000).
The mantissa is m = 1 + [000b / 23] = 1
The exponent is e = 0000b - 1000b = -8
The result is (-1)0 x 1 x 2-8 = 1/256 = 0.0039
The above example is the smallest (non-negative) value that we can represent. While this is not extremely close to zero, keep in mind that this is for an 8-bit floating point value. In practice, most floating point representations have sufficient bits in the exponent to represent non-zero numbers that are quite small. For instance, the IEEE Single Precision floating point standards uses thirty-two bits with eight bits for the exponent. It would therefore be able to represent numbers as small as 2-128 (3 x 10-39) using the representation scheme we have developed thus far. A strong argument can be made that this is sufficiently close to zero for any purpose for which it would be reasonable to use a single precision floating point representation.
So what are the remaining deficiencies that this version of our floating point representation has?
First, we still cannot exactly represent zero. While we might think that we could probably live with the fact that we can't exactly represent zero, it turns out that it is actually rather useful from a programming standpoint if our floating point representation can exactly represent at least a limited range of integers, including most especially zero. In fact, the people that developed the floating point standards that we are working up to stipulated that the single precision floating point representation had to be able to exactly represent all of the integers that could be represented by the single precision integer representation.
Second, by using a signed-binary representation for the mantissa the magnitude comparison task has gotten a bit trickier. There is no problem for positive values and we can use the exact same hardware that we did for integer representations. But for negative values we have to add some additional logic for cases where the exponents in the two numbers being compared are the same. Remembering that all engineering involves compromises, we choose to accept the added burden - which is actually quite small - in exchange for the much simpler and faster negation ability. So this is no longer a deficiency, but instead an artifact of the representation that we have chosen to accept.
The sole remaining deficiency that we need to correct is the inability to exactly represent zero. So how do we achieve this?
Keeping in mind that the problem was caused by that hard-coded '1' due to the normalization of the mantissa, we look for a solution by seeing if we can "turn off" that normalization under the conditions where it is causing problems. What if we impose a special case where, for the smallest exponent, we assumed instead that the first digit was a zero? By "denormalizing" the mantissa for this one value of the exponent, we have turned the representation into a fixed point representation.
Floating Point Representation #4
| b7 | b6 | b5 | b4 | b3 | M3 | (rp) | b2 | b1 | b0 |
| S | E3 | E2 | E1 | E0 | ? | . | M2 | M1 | M0 |
Note: Only the bits labeled bn are actually stored.
Sign Bit (s): S
Mantissa (m):
if (E3:E0) = 0000:
m = 0 + [three-bit signed integer (M2:M0) divided by 23]
else
m = 1 + [three-bit signed integer (M2:M0) divided by 23]
Exponent (e): four-bit offset binary integer (E3:E0) - 1000b
Value = (-1)s x m x 2e
Now if every bit in the mantissa is zero - and if we use the smallest (most negative) value for the exponent since that is the only time we assume a leading '0' on the mantissa - we have an exact representation for zero. Furthermore, because we used an offset binary representation for the exponent, the smallest exponent is represented by all 0's and hence it turns out that a pattern of all zeroes is exactly zero regardless of whether we are dealing with unsigned integers, signed integers, or floating point values.
It should also be pointed out that we still have exactly zero even if the sign bit is a '1'. So we have both a "positive zero" and a "negative zero".
Another nice result is that having the fixed point representation available to us for the smallest values is that we increase the static range considerably - namely by the number of bits actually stored in the mantissa. For instance, in our current representation the smallest positive value we can represent is now:
Example:
Problem: What is the smallest strictly positive value that can be represented?
Solution: The pattern for this value would be 0000 0001.
Grouping the bits into their logical groupings, we have (0)(0000)(001).
The mantissa is m = 0 + [001b / 23] = 0.125
The exponent is e = 0000b - 1000b = -8
The result is (-1)0 x 0.125 x 2-8 = 1/8 x 1/256 = 0.00049
Notice that this value is smaller that the smallest representable value in our previous version by a factor of eight.
Life appears good but we have introduced a new problem. We have created a gap in the range of numbers that we can represent because we jump from:
0000 0111 = (0)(0000)(111) = 0.1112 x 2-8 = 0.003418
to
0000 1000 = (0)(0001)(000) = 1.0002 x 2-7 = 2-7 = 0.007813
as we change from the smallest exponent to the second smallest exponent. That's a change by more than a full factor of two without being able to represent any value in between. Consider the consequences for our dynamic range at this point.
To see this gap more closely, consider the next values on either side of it:
0000 0110 = (0)(0000)(110) = 0.1102 x 2-8 = 0.002930
0000 0111 = (0)(0000)(111) = 0.1112 x 2-8 = 0.003418
0000 1000 = (0)(0001)(000) = 1.0002 x 2-7 = 2-7 = 0.007813
0000 1001 = (0)(0001)(001) = 1.0012 x 2-7 = 2-7 = 0.008789
The difference between the first pair - the largest pair where both numbers are below the gap - is 0.000488 (2-11) and the difference between the last pair - the smallest pair where both numbers are above the gap - is 0.000976 (2-10). But the difference between the middle pair - the pair that spans the gap - is 0.004395 (basically 2-8).
So we still have a deficiency in our representation. Like the inability to exactly represent zero, it might be tempting to ignore this problem and, in most applications, we would probably never encounter a problem as a result. But, like the inability to exactly represent zero, it turns out that we do not want to leave this deficiency uncorrected because, sooner or later, it will come back to haunt us.
The solution to out remaining deficiency - the loss of dynamic range as we cross the gap from an implied '0' to and implied '1' for the lead bit of the mantissa - is to have the two smallest exponent representations represent the same actual exponent. The difference is that the smallest representation has an implied '0' for the first bit of the mantissa and the second smallest, as well as all others, has an implied '1' for this bit.
Floating Point Representation #5
| b7 | b6 | b5 | b4 | b3 | M3 | (rp) | b2 | b1 | b0 |
| S | E3 | E2 | E1 | E0 | ? | . | M2 | M1 | M0 |
Note: Only the bits labeled bn are actually stored.
Sign Bit (s): S
if (E3:E0) = 0000:
Mantissa (m): m = 0 + [three-bit signed integer (M2:M0) divided by 23]
else
Mantissa (m): m = 1 + [three-bit signed integer (M2:M0) divided by 23]
Value = (-1)s x m x 2e
It should be noted that the values having an implied zero in their representation do not have as good a dynamic range as the rest of the floating point values. The reason becomes fairly evident when you consider that a number with an implied one as the leftmost bit in the mantissa always has the full number of bits in the stored mantissa to draw upon as significant bits. But for a number having an implied zero as the leftmost bit, the number of significant bits is reduced by the number of stored zeroes at the left of the mantissa that are there only to act as place keepers in the fixed-point representation used for these values.
Our representation above is very close to the actual floating point representation specified by the Institute of Electrical and Electronic Engineers (IEEE). In fact, there are really only two differences.
First, because of the increase in static range at the small end of the representable values, the IEEE elected to represent an exponent of zero by the pattern having a leading '0' and the rest of the bits '1'. This is only a shift of one in the pattern from what we developed above.
So, for our 8-bit representation above, it means that an exponent of zero is represented as 0111 instead of 1000. Therefore to get the actual exponent we would subtract seven (0111) from all exponents (when initially interpreted as an unsigned integer) except for the smallest one (pattern 0000). Since the next-to-smallest exponent (0001) has an actual value of:
(00012) - 710 = -610
the smallest exponent (0000) will have this same value.
The second difference is that the IEEE chose to interpret some of the patterns as special codes instead of as floating point values. This permits error detection and for errors, such as overflow conditions and division by zero, to propagate their way through a series of floating point operations so that they may be detected in the final result.
To do this, they used the largest exponent (all 1's) as a special flag. With this exponent, if the mantissa is exactly zero then the interpretation is that the result is "infinity", with "plus infinity" and "minus infinity" being distinguishable by the sign bit. For any non-zero mantissa the interpretation is that the result is "Not A Number" or "NAN" for short. This might result from trying to take the square root of a negative number, for instance.
If the IEEE recognized an 8-bit floating point format, the following would be it's specification.
IEEE-compliant Floating Point Representation
| b7 | b6 | b5 | b4 | b3 | M3 | (rp) | b2 | b1 | b0 |
| S | E3 | E2 | E1 | E0 | ? | . | M2 | M1 | M0 |
Note: Only the bits labeled bn are actually stored.
Sign Bit (s): S
if (E3:E0) = 1111:
(0)(1111)(000) = +infinity
(1)(1111)(000) = -infinity
any other pattern is NaN
if (E3:E0) = 0000:
Mantissa (m): m = 0 + [three-bit signed integer (M2:M0) divided by 23]
otherwise:
Mantissa (m): m = 1 + [three-bit signed integer (M2:M0) divided by 23]
Value = (-1)s x m x 2e (value not defined for +/- infinity or NaN)
So let's see if we can use this knowledge to interpret and create floating point representations for one of the actual IEEE formats.
The single precision format has a total of 32 bits including an 8-bit exponent.
This short description, plus the knowledge gained up to this point, is all that we really need to know.
We know that:
Furthermore, we know the following about the exponent:
And we know the following about the mantissa:
Finally, we know we can work with the mantissa as a fixed point value:
Most people have a lot of difficulty determining the floating point representation for a number or what number is represented by a particular floating point pattern. By understanding what the representation means, in the context of how it was built up, combined with an understanding of how to work with fixed point and offset binary representations, you can make this process very straight forward.
Example:
Problem: Convert π to its IEEE Single Precision format:
The number is positive, so the sign bit is zero.
To get the bits in the mantissa, we first multiply the value being converted by 223:
Using a calculator, 223π is 26353589 to the nearest integer.
The hexadecimal representation of this integer is 0x01921FB5
The binary pattern for this is: 0000 0001 1001 0010 0001 1111 1011 0101
This pattern has 25 significant digits. To get it to have 24 (a leading '1' plus the 23 bits that will get stored) we have to divide it by 2. That means that the exponent has to increase by 1 to counter act this.
An exponent of zero has a pattern of 0111 1111, so an exponent of 1 has a pattern of 1000 0000.
The final binary pattern is therefore
π = 0100 0000 0100 1001 0000 1111 1101 1010 = 0x40490FDA
Example:
Problem: Convert the result of the previous example back into a decimal value:
Breaking the representation into its sign, exponent, and mantissa components:
(0) (1000 0000) (?100) (1001) (0000) (1111) (1101) (1010)
The final quantity is positive.
The question mark represents the implied bit. Since the exponent pattern is not zero, the implied bit is 1.
The full mantissa is therefore:
(1100) (1001) (0000) (1111) (1101) (1010) = 0xC90FDA
Converting this to an decimal integer: 0xC90FDA = 13,176,794
The exponent is: (1000 00002) - 127 = 0x80 - 127 = 128 - 127 = 1
The final value is v = (13,176,794 / 223) * 21 = 13,176,794 / 222 = 3.1415925
The double precision format has a total of 64 bits including an 11-bit exponent.
Based upon our understanding of the IEEE floating point representation scheme, answer the following questions (in decimal):
As we did in the single precision case, we will first summarize the characteristics of this representation. But this time we will be a little more explicit in showing the link between our understanding of the desired characteristics and how we can use that understanding to build up the details of the representation from scratch:
We know that the whole representation is based upon an exponential format where we have a mantissa and an exponent.
Desired Feature: The ordering of values should depend on the bits from left to right, just as in an integer.
From this know that:
Because the sign bit and the mantissa are separated from each other, it makes sense that:
Since we want the ordering to proceed from the most negative exponent to the most positive exponent, we know that:
We would normally expect an exponent of zero to be 1...000 but the IEEE committee chose to use a value one less than this. We can remember this little fact a number of ways. We can remember that an exponent of "1" is represented as a leading '1' followed by all '0's. Alternatively, we could remember that for an n-bit exponent that zero is the largest binary pattern for n-1 bits. Yet another way is to recognize that the value we subtract off also happens to be equal to the largest exponent we can represent (after taking into account the fact that an exponent of all ones is a special flag value and not an actual exponent). Whatever makes the most sense to you is what you should use. The end result is that for this representation:
Likewise, the desire for proper ordering requires that we use a normalized exponential notation such that:
Because the stored part of the mantissa is a fixed point value with the binary point all the way to the left:
Desired Feature: We want to be able to exactly represent zero.
This leads us to de-normalize the mantissa for the smallest exponent, with the following result:
Desired Feature: We want to be able to trap special error conditions.
Since an exponent pattern of all zeroes is used to represent zero, we use the exponent pattern from the opposite end as our flag value:
One of the things we want to flag is infinity. We represent this case as a mantissa with all zeroes. We can remember this because, at least compared to NaN, it can almost be thought of as a specific value and therefore should have a specific representation. We can also think of it as the result of dividing by zero and so we use a mantissa of zero. Again, use whatever makes sense to you. The end result is that:
So now let's answer our questions.
This would be an all zero exponent and a single 1 at the right of the mantissa. So
value = 1 x 2-52 x 2-1022 = 2-1074 = 4.94 x 10-324
The mantissa is all ones which, combined with an implied leading '1', is essentially 2.0
The exponent is all ones except the last bit, so it is (211 - 2) - 1023 = 1023
value = 2.0 x 21023 = 21024 = 1.80 x 10308
The value one has just the implied '1' and a stored mantissa of all zeroes. The smallest value by which we can change this is to make the right most mantissa bit a one. This is a change in value of:
x = 1 x 2-52 = 2.22 x 10-16
The static range is the largest value divided by the smallest value (in terms of magnitude):
static range = 21024 / 2-1074 = 21098 = 3.4 x 10330
The dynamic range is 1/x where x is the answer from question #3.
dynamic range = 1/x = 252 = 4.5 x 1015
By simplified example, 1.00 has two sig figs. The smallest change we could represent would be 0.01 and so our dynamic range would be 102. So, the number of sig figs is the base-10 log of the dynamic range.
sig figs = log10(4.5 x 1015) = 15.7 (roughly sixteen)
Any integer representable by the bits in the mantissa (including the implied leading '1') can be represented exactly. The upper limit is approached when we have a mantissa that is all ones and an exponent that is just large enough to make this an integer. But if we add one to this, we end up with an all zero mantissa (except for the implied '1') and an incremented exponent. This is still exactly represented. However, the right most bit of the mantissa is now the 2's bit (instead of the 1's bit) and so we can't add just one and still represent it exactly.
Again using a simplified example, if we had three bits stored in the mantissa:
1.111 x 23 + 1 = 1.000 x 24
So, for our present representation, the largest continuous integer would be
n = 253 = 9,007,199,254,740,992.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | |
| 0 | NUL | SOH | STX | ETX | EOT | ENQ | ACK | BEL | BS | HT | LF | VT | FF | CR | SO | SI |
| 1 | DLE | DC1 | DC2 | DC3 | DC4 | NAK | SYN | ETB | CAN | EM | SUB | ESC | FS | GS | RS | US |
| 2 | SP | ! | " | # | $ | % | & | ' | ( | ) | * | + | , | - | . | / |
| 3 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | : | ; | < | = | > | ? |
| 4 | @ | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O |
| 5 | P | Q | R | S | T | U | V | W | X | Y | Z | [ | \ | ] | ^ | _ |
| 6 | ` | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o |
| 7 | p | q | r | s | t | u | v | w | x | y | z | { | | | } | ~ | DEL |
In the above table, the upper (most significant) nibble is in the leftmost column which the lower (least significant) nibble is in the top row. For instance, the ASCII code for the letter 'G' is 0x47.
Most of the first thirty-two codes are control codes for equipment no longer in use today. As a result these codes are seldom seen in practice anymore. But a small subset of the control codes are still used.
| HEX | Decimal | CODE | Name |
| 0x00 | 0 | NUL | Null Character |
| 0x07 | 7 | BEL | Bell (Buzzer) |
| 0x08 | 8 | BS | Backspace |
| 0x09 | 9 | HT | Horizontal Tab |
| 0x0A | 10 | LF | Line Feed |
| 0x0B | 11 | VT | Vertical Tab |
| 0x0C | 12 | FF | Form Feed |
| 0x0D | 13 | CR | Carriage Return |
| 0x1B | 27 | ESC | Escape |
| 0x20 | 32 | SP | Space |
| 0x7F | 127 | DEL | Delete |
While the ability to represent numerical values in a computer is critical, there is another type of data that is extremely also extremely important - text. Just as we did with the numerical data types, we need to devise a means of representing textual information in some form of binary format since that is the only format available to us in a computer.
If you are like many people, at some point while you were growing up you exchanged "secret messages" with a friend using a code where you represented the letter 'A' by the number '1' and so forth ending with 'Z' being represented by the number '26'. In essence, you were encoding text information as numbers and storing those numbers on some type of media (a piece of paper). You then gave that media to someone else who interpreted the numbers stored there according to that same code and, as a result, was able to recover the original text information. The means that we store text in computer memory is almost identical to this approach.
The most common code for text in use today is the American Standard Code for Information Interchange, or ASCII for short (pronounced ask-key). The ASCII code was developed in the 1960's for the purpose of permitting data processing equipment, such as teletypewriters, to communicate with each other. It was determined that seven bits were necessary to provide enough codes for all of the characters, numbers, and punctuation marks found on a standard typewriter keyboard plus permit a host of special codes used to control how the data was displayed on the receiving equipment or other aspects of the data transmission and reception.
Since almost all machines today are centered on the eight-bit byte, we use a single byte for each ASCII code with the most significant bit set to zero. Most machines also support an second set of characters that have the most significant bit set to one. Unfortunately, these "extended" characters are not standardized and vary greatly from machine to machine and even compiler to compiler. It is best to avoid the use of these extensions unless you are willing to accept the extreme compatibility and portability limitations that will result.
In the C programming language, surrounding a character by a pair of single quote marks is a convenient way of representing the ASCII code for that character.
Example: What values are stored at the relevant memory locations if 'A' is stored at memory location 0xC000, 'a' is stored at 0xC001, and the result of the expression ('a' - 'A') is stored at location 0xC002?
Solution: 'A' is 0x41, 'a' is 0x61, so ('a' - 'A') is 0x20.
- 0xC000: 0x41
- 0xC001: 0x61
- 0xC002: 0x20
Being able to represent individual characters as specified memory locations is very useful, but it is not very convenient for the way we normally want to work with text information. Typically, when we work with text, we work with "strings" of characters. The obvious way to represent a string in memory is as a string of ASCII codes - and this is exactly what is done.
But there is a subtlety that we have to deal with - how do we know where the string ends? We have two options - we can either always tell keep track of both the address where the string starts and how long the string is, or we can just keep track of where the string starts and embed a "delimiter" in the string data itself to mark the end of the string. The most common - but by no means the only - means of delimiting strings is to place the NUL character (0x00) after the last actual character in the string. This is, not surprisingly, referred to as a "null terminated string".
Just as the ASCII code for an individual character is expressed by surrounding the character by single quotes, a string of ASCII codes, including the delimiter, is expressed by surrounding the string of characters by double quotes.
Example: The string "ECE-1021 Module #1" is stored at location 0xDC08. Draw the relevant memory map using.
0 1 2 3 4 5 6 7 8 9 A B C D E F 0xDC ?? ?? ?? ?? ?? ?? ?? ?? 'E' 'C' 'E' '-' '1' '0' '2' '1' 0xDD SP 'M' 'o' 'd' 'u' 'l' 'e' SP '#' '1' NUL ?? ?? ?? ?? ?? The above uses the characters to represent the memory, and this is generally the quickest and most useful way of representing the codes. For completeness, the actual values (in hex) are shown below.
in hex 0 1 2 3 4 5 6 7 8 9 A B C D E F 0xDC ?? ?? ?? ?? ?? ?? ?? ?? 45 43 45 2D 31 30 32 31 0xDD 20 4D 6F 64 75 6C 65 SP 23 31 00 ?? ?? ?? ?? ??
If we have a representation that consists of more than one byte, in what order are those bytes stored in memory? This is far from being a trivial question. Consider, for example, the following snapshot of portion of memory:
| ADDRESS | C32E | C32F | C330 | C331 | C332 | C333 | C334 | C335 | C336 | C337 |
| CONTENTS | F3 | FF | DA | 0F | 49 | 40 | 2E | 00 | 21 | 13 |
Note: All values in hex
Each memory location is capable of storing a single byte of data, so if our value is represented using more than one byte, there has to be agreement on how those bytes are stored and how we refer to them. When we indicate where a value is stored, we seldom specify the entire range of memory locations that are used. Instead, we give the address of a single byte and it is understood that the value is stored in consecutive memory locations beginning at that address.
For instance, let's assume that we have stored the a particular value using a two-byte signed integer representation and stored it at memory location 0xC336. What does this mean? Is the address the location of the most significant byte, or the least significant byte? Is it the smallest address in the block of memory, or the largest? Is the value stored with the most significant byte at the largest address, or at the smallest? Clearly there are several possible conventions and unless everyone is in agreement on which one is actually used, we are in serious trouble.
So how many conventions are we really dealing with? It turns out that there are four, based on the possible combinations of whether the specified address is for the MSB or the LSB and whether the byte located at the highest address is the MSB or the LSB. For our two-byte signed integer stored at 0xC336 this leaves us with:
| Convention | Address | high address | C335 | C336 | C337 | hex | dec |
| 1 | MSB | MSB | LSB | MSB | xxx | 0x2100 | 8448 |
| 2 | MSB | LSB | xxx | MSB | LSB | 0x2113 | 8467 |
| 3 | LSB | MSB | xxx | LSB | MSB | 0x1321 | 4897 |
| 4 | LSB | LSB | MSB | LSB | xxx | 0x0021 | 33 |
You can see that which convention is used has an enormous impact on what value is retrieved from memory.
Of the four possible conventions, only two are found in common use. These two have one characteristic in common - the address specified as the data's location is the "base address" and all other addresses in the representation are at higher locations. This characteristic eliminates Conventions #1 and #4 from the above table.
Of the remaining two conventions, we can distinguish them by noting that in Convention #2 the "end" of the value (the LSB) is at the "big" address. Conversely, in Convention #3 the "end" of the value (the LSB) is at the "little" address. These observations lead to the descriptive names that are generally used for the two conventions - Convention #2 is referred to as "Big Endian" and Convention #3 is referred to as "Little Endian".
Another way of interpreting the names Big Endian and Little Endian is that in a Big Endian representation, the "big" part of the value (the MSB) is at the "end" of the address space. Conversely, in the Little Endian format the "little" part of the value (the LSB) is at the "end" of the address space. Here you just have to remember that "end of the address space" means the smallest valued address.
Storage Conventions for an n-byte value
| Convention | Base Address + 0 | Base Address + (n-1) |
| Big Endian | MSB | LSB |
| Little Endian | LSB | MSB |
Each convention has its share of supporters and critics. Because Motorola (and therefore the Mac) uses Big Endian while Intel (and therefore the PC) uses Little Endian, the arguments of both sides sometimes appear to be pronouncements of religious conviction rather that statements of technical merit. As you should already suspect, the reason that no single convention has gained universal acceptance is because each convention has advantages and disadvantages compared to the other. For instance, in a Big Endian machine, magnitude comparisons can be performed starting with the base address; whereas in a Little Endian machine, most arithmetic operations can be performed starting with the base address.
Up to this point we have assumed that the values stored in memory have been stored using a particular representation and read using that same representation. This is almost always the case. But it is possible to store values using one representation and read them using another. After all, there is nothing to distinguish the bit pattern for an integer from the bit pattern for a floating point value - they are simply patterns of 1's and 0's stored in memory.
Although sometimes we "cross represent" values intentionally, it is usually the result of an error on the programmer's part. No matter how diligent we might be, these types of errors are more common than we would prefer. People that understand number representation and how it is implemented have the ability to identify and correct these errors expeditiously, whereas people that are ignorant of these topics can literally spend hours or even days baffled by a simple mistake caused by a single wrong character in a print statement.
Probably the most common example of cross-representation in C involves the input and output routines. For instance, the programmer wants to get a four byte signed integer from the user but mistakenly tells the input routine to store the value entered as a single precision floating point value. The person then, on the next line, echoes the value that the user entered by invoking the output routine and has properly told it that the value is supposed to be a four-byte signed integer.
Example:
Problem: The programmer declares that a two-byte signed integer is to be stored at address 0xC300. The machine uses the Little Endian format. After prompting the user for such an integer, the user enters the value "123456". The programmer then echoes the value back out to the user. However, the programmer has mistakenly told the input routine to store the entered value as an IEEE single precision floating point value. What value is reported back to the user?
Solution: The user is going to enter the value 123456 and that is going to get stored as a 4-byte floating point value with and eight bit exponent and a twenty-three bit mantissa. Because only the very smallest values have an implied leading '0', this representation will have an implied leading '1'.
Converting this value to binary we get:
12345610 = 1E240H = 1 1110 0010 0100 0000 b
Normalizing this value we get:
1 1110 0010 0100 0000 b = 1 . 1110 0010 01 b x 216
Building up our floating point representation:
sign bit = 0
exponent = 16 + 127 = 143 = 0x8F = 1000 1111 b
mantissa = 111 0001 0010 0000 0000 0000 b
pattern = (0)(1000 1111)(111 0001 0010 0000 0000 0000)
pattern = 0100 0111 1111 0001 0010 0000 0000 0000 = 0x47F12000
The base address is 0xC300 so the four bytes are stored at locations 0xC300:0xC303
The Little Endian format means that the LSB is at the little address, so the pattern is stored as follows:
| ADDRESS | C2FE | C2FF | C300 | C301 | C302 | C303 | C304 | C305 | C306 | C307 |
| CONTENTS | ?? | ?? | 00 | 20 | F1 | 47 | ?? | ?? | ?? | ?? |
Note: All values in hex
When these memory locations are read for output, they will be interpreted as a two-byte signed integer starting at 0xC300 and stored in Little Endian order. The resulting integer that is displayed will therefore be:
value = 0x2000 = 819210
So how to you detect this kind of mistake? Certainly, it can be difficult. In this example, the reported value turned out to be considerably smaller than the entered value; but in practice there is virtually no predicable pattern to the observed behavior - at least not predictable until you have identified the exact error involved. But a common trait that is exhibited by cross-represented values is that changes to the program or data that should produce only small changes in the output produce wildly erratic changes in the results. This makes since when you consider that a small change in an integer might result in a large change in a floating point value because what changed was one of the bits in the exponent.
A lot of information has been presented in this Module. As much as possible, the viewpoint used in presenting the material was from a problem solving approach. This is particularly evident in how the IEEE floating point format was introduced. While most texts present the final result - if they present it at all - along with a recipe on how to use it, such as approach does little to foster your understanding of why the format is the way it is. Without this understanding, you would be relegated to using rote memorization - a tactic that quickly becomes counterproductive in the field of engineering. Even more importantly, for the purposes of this course, such a presentation would have conveyed little about the steps used in solving engineering problems.
The author would like to acknowledge the following individual(s) for their contributions to this module: