(Last Mod: 27 November 2010 21:38:37 )
Algorithms are basically a set of instructions that, if correct and if followed carefully, produce some desired result. Since they are sets of instructions, they are generally presented in such a way that that the step-by-step nature of how they should be followed is readily apparent. The two most common representations are pseudocode and flowcharts. In this course, unless it is stated otherwise, you are free to use either one at your discretion. Likewise, unless the context indicates otherwise, references to either in the following discussion generally refer to both.
Algorithms can be thought of as the recipe for taking the general solution for a class of problem and applying it to a specific instance of a problem covered by that class. For instance, the class of problem might be to find the surface area of a sphere given its radius. Through some problem solving means - perhaps by performing the fundamental calculus computation or perhaps simply by looking up the equation in a math book - we determine that the general solution to the problem is that the area is four times pi times the square of the radius. We can then use this general solution and create an algorithm that permits use to compute the surface area of a specific sphere:
But our problem could be at an even more abstract level than this - perhaps the problem is to find the surface area of a solid of rotation for a function that intersects the x-axis in exactly two places. In this case, a sphere is simply a specific instance of the problem where the function happens to be:
y = sqrt(r2 - x2)
Now the algorithm might look something more like this:
Notice that we still only have a set of tasks, but each task is more narrowly defined and can be treated as its own problem and a more detailed algorithm for that task developed independently. Notice also that two of the tasks are intimately related such that figuring out how to solve the first can be expected to directly lead to knowing how to solve the second.
Note how the word "TASK" is used above. A line that starts with this word contains a description of something that needs to be accomplished as opposed to an instruction, such as "GET" or "SET" in the first example, that tells us how to actually accomplish it. The process of breaking down a problem into a set of tasks is frequently referred to as decomposing the problem and the result is generally called a "decomposition outline". At some point, a given task is so thoroughly refined that any further decomposition almost has to involve specific instructions on how to perform the task. Some people maintain that at this point you have moved from writing a decomposition outline to writing pseudocode. Others maintain that the phrases "decomposition outline" and "pseudocode" are largely interchangeable. This latter school of thought makes a strong argument when they point to the analogous situation when this same process is done graphically. Whether it is at the highest level of abstraction or the deepest level of detail, we call the result a "flowchart". We might use adjectives such as "top-level" or "highly-detailed" to indicate the degree of abstraction represented in the flowchart, but we don't usually claim that there is something fundamentally different between the two.
What everyone pretty much agrees on is that, whatever you call it, there is a continuum in the tradeoff between remaining very abstract versus being highly detailed and the proper balance depends on the specifics of the situation. For instance, Task 1.1 above - finding the left hand intersection - may well be adequately refined if it can be reasonably assumed that the person using the outline is capable of going from there and figuring out, on their own, how to find that intersection. The purpose of the outline is to tell them that finding the point of intersection is something that needs to happen and not how to go about finding it. If that is not a reasonable expectation, then that task should be further refined. Hence, if you are asked to develop a flowchart or write the pseudocode for a problem, it is best to come to an understanding of how much detail is expected. Fortunately, unlike in a classroom setting, the answer to this question is usually self-evident to a large degree. The reason is simple - in most cases where you might be asked to do this, you also know why you are being asked to do it and therefore you know the context in which your work will be used. You will probably also have some sort of feedback so that if you aren't sufficiently detailed you will be asked to go into more depth whereas if you are going into too much detail your boss will start asking what's taking so long - although, in practice, they may do that anyway even in the same breath in which they request more detail.
As mentioned previously, algorithms are generally represented by either pseudocode or a flowchart. But what are these? It might be accurate to claim that each is merely a means of representing an algorithm, but that would hardly move the discussion along. Instead, let's focus on what features we need our means of algorithm representation to have in order for it to be a meaningful and useful representation.
One of the most difficult things for people just learning problem solving - especially when it involves computer programming - is to clearly distinguish between the concept of problem logic and implementation logic. The former is independent of the details of how the problem solution is implemented. If you are trying to find the radius of a sphere having a specific surface area, then you need to find out what that area is, you need some means of dividing that area by 4pi, and you need some means of taking the square root of the result. It doesn't matter whether you are solving the problem with a C program, a Java program, a calculator, a pencil and paper, or in your head - those elements are part of the logic of solving the problem. The logic involved in taking the square root of a number, on the other hand, is germane primarily to the logic of how you are implementing your solution. In other words, for most purposes I can communicate the logic behind how to determine the radius of a sphere with a specific surface area by going into no more detail than to note that, at some point, it is necessary to take the square root of a number.
Your algorithm representation should focus on the logic of the problem, and not the logic of the eventual implementation. More specifically, the upper levels of your representation should, to the degree possible, be devoid of implementation details - these should be relegated to the lower levels of the representation.
Most problems, especially if they are intended to be solved with the aid of a computer program, involve flow control. In the "structured programming" paradigm, this flow control consists of sequences, selections, and repetitions. This may not be readily apparent at the topmost level where the algorithm can be represented by a list of tasks that are to be performed one after another in a specific sequence. But at some point, as each of those tasks is developed, decisions will have to be made and different steps taken depending on the outcome of those decisions. The representation method used should be compatible with this and clearly show the points at which decisions are made and what the various courses of action are that can result.
Our algorithm representation should be flexible and allow us to readily collapse it so as to show less detail and focus on the more abstract elements of the algorithm or to expand it so as to get as detailed as necessary in order to actually implement the solution. Unstated in this is an acknowledgement that, as we expand our algorithm and become more detailed, at some point we have to get into the logic of the implementation issues.
For instance, if we expand the step that says to take the square root of a number, we have to start describing the specific method that will be used to do this and that method is highly dependent on the eventual implementation. At that point, our algorithm is becoming "locked" to that particular implementation. This is perfectly acceptable. The reason that we should be asking for more detail on how to take the square root is because we are now dealing with implementation issues and therefore expect that the steps will be specific to the implementation.
If we have structured our representation properly, then we can always back up. If our original implementation was with a C program and now we want to implement the algorithm in assembly on a PIC microcontroller, then we simply collapse our algorithm until the implementation dependent portions are gone and then re-expand the high level logic that was left in such a way that it can now be implemented on a PIC. If our high level logic is geared towards a particular implementation and our problem-oriented tasks are contained at lower levels, then this because very difficult to do.
At the end of the day, the goal is usually to actually implement a solution to the problem being solved. If our method of representing our algorithm does not lend itself to an orderly implementation of that algorithm, then our method is seriously flawed. Conversely, if our method of representation lends itself to a systematic implementation of the algorithm, then our method is extremely useful.
By "systematic implementation" we mean that we should be able to take our represented algorithm and break it into easily identifiable fragments each of which can be readily translated into one of the structures, such as a while() loop or an if()/else block, available to us in our chosen implementation scheme be it a C program, an assembly language routine, an electronic circuit, or a physical mechanism.
This is one of the reasons why we seldom use flowcharts for algorithms that are slated for implementation using a physical circuit - flowcharts do not lend themselves to aiding such an implementation. But schematics do and properly developed schematics possess all of the properties described above. Likewise, schematics are seldom used to develop algorithms slated for implementation with a computer program for the same reason. However, when collapsed to their most abstract level - the topmost level or two - a well-structured flowchart and a well-structured schematic for a program and circuit, respectively, that solve the same problem may will look nearly identical. The reason is that, in each case, the topmost levels are representing only the logic of the problem and do not contain much, if any, information specific to the eventual means of implementation.
From this point forward, we will restrict the discussion to algorithms that are intended for eventual implementation using a computer program - but the concepts described can be readily generalized to any type of implementation and you should read them with the intent of grasping those generalized concepts.
Most texts maintain that the pseudocode or flowchart for a problem should represent the solution in a manner that is independent of how that solution will eventually be implemented and sufficiently complete such that the person developing the conceptual solution, who may have little if any programming background, can turn the material over to a programmer who could, in turn, decide what programming language to use and proceed to implement the solution without even understanding any of the conceptual goals behind the code being written. For instance, I should be able to give you a flowchart for a function that accepts one value and that then uses that value to produce and return another value. If I have done my job adequately, you should be able to write the function to accomplish this task in any language you are familiar and comfortable with without ever knowing or caring that the function is actually implementing a Bessel Function of Order Zero using truncated Chebyshev polynomials.
But such a philosophy is needlessly restrictive and fails to recognize some important realities. As discussed in the previous sections, some effort should be put into making the upper levels of the represented algorithm implementation independent. If it is practical to halt the expansion of the algorithm at the point where dealing with implementation specifics is feasible - great. This is likely to be the case if the the purpose of the given flowchart or pseudocode is to communicate the overall approach to a potential investor or an end-user. But generally it is necessary to carry the algorithm development at least a bit further - to step over the "implementation boundary" far enough that the people actually implementing and testing the code can be confident that the level of detail has truly made it into "their world" and that they are dealing only with implementation issues and not problem logic issues.
In point of fact, in the "real world" pseudocode and flowcharts are used in a variety of ways. On rare occasion reality and ideality actually come close to each other and they are used precisely as described above in the Bessel Function example. But, flowcharts also commonly serve as formal documentation for the high level structure of programs and, when used as such, generally offer very little detail but, instead, illustrate the overall flow of the program. In these cases, avoiding implementation details is usually pretty important. Other times they are used specifically to show the detailed steps necessary to carry out a specific implementation and, when used this way, are completely dependent on the language and, perhaps, even the processor being used. For instance, the algorithm could be for a new means of computing trigonometric functions using the latest processor instructions so as to increase speed and reduce memory usage. Such an algorithm is fundamentally tied to the implementation - but then so is the very problem that is being solved. The problem isn't how to compute the value of the sine of an angle, the problem is how to efficiently use the latest processor resources to compute the value of the sine of an angle - a subtle but critical distinction.
However, the vast majority of cases falls somewhere between these two extremes. From a code development point of view, pseudocode and flowcharts are generally very informal and incomplete - their purpose is to guide the programmer's thoughts just far enough to enable them to proceed with the coding directly. This is particularly the case when the person writing the pseudocode and the person writing the source code are one and the same but it is also quite common even when one person (or team) is preparing the flowcharts and another person (or team) is writing the code, especially if there is good communication back and forth. It is not uncommon to see a flow chart that is very chaotic in that one section has virtually no detail while other parts are documented in excruciating detail. The sparse sections probably represent portions where the programmer is comfortable with the tasks and needs very little guidance while the highly detailed sections are probably where the programmer is unfamiliar with the concepts or having a difficult time getting correct results.
Just like in the "real world", the guidelines in this course reflect the purposes of the pseudocode or flowchart being submitted - and there are two of them. In addition to guiding your own code development efforts, what is submitted must also serve to satisfy the grader that you have an adequate understanding of the problem being solved and have a viable approach to its solution. Keep in mind that the grader's sole insight into whether you know how to perform a particular task is what you have presented. The grader is not a mind reader and is not expected to make any effort to become one. A useful guideline for how detailed your pseudocode or flowchart should be is that it should be reasonable for you to hand it to another student in the course who is about average in their performance and who has been keeping up with the material to date (but no further) and expect them to be able to implement the code with little or no difficulty even if they have not seen the problem previously.
Imbedded in this guideline are a few subtleties. As we reach new material, your pseudocode and flowcharts should be more detailed with regards to that material than it needs to be when dealing with material from considerably earlier in the course. It will be understood (hoped?) that your programming skills are improving and that your pseudocode and flowcharts don't need to be as detailed about material that you should be familiar with. However, if your source code demonstrates that you are not yet adequately comfortable and proficient with a particular topic, don't be surprised to lose points for inadequately detailed pseudocode or flowcharts. In general you will not lose points for presenting your pseudocode/flowcharts in too detail.
As mentioned previously, pseudocode is ideally language independent, however the reality is that all of the pseudocode you write in this course will be used to implement source code in a specific programming language, namely C. It is therefore permissible for you to use C statements and constructs in your pseudocode and flowcharts. By similar reasoning, it is NOT permissible to use statements and constructs from Matlab, Basic, Java, or any other language you might be familiar with. This is not to say that you can't use these in pseudocode or flowcharts that you are using strictly for yourself (how would we know, anyway?) but only that the pseudocode you submit for grading must be free of them. Be aware that there is a danger to using language elements within your pseudocode - which is one of the reasons why the use is generally frowned upon. By using language elements it becomes very easy to lose focus on representing the logic of the problem solution and begin focusing on the logic of the implementation. Keep in mind that pseudocode and flowcharts are not simply another way of expressing your program - they are to represent the logic behind how the problem is solved.
Even if you don't use actual C statements within your pseudocode or flowchart, it is highly encouraged that the structure of your algorithm be laid to match the control structures available to you in C. Doing so will drastically decrease the amount of time you spend converting the algorithm to viable C code.
To a much greater degree than programming style guidelines, there are very few commonly accepted standards for how pseudocode is written. This generally reflects the fact that it is used primarily as a rather short-term communication between members working on a specific project - the code itself and other documents are used for long-term archival purposes. Where those other documents use algorithm representations, flowcharts tend to be the preferred means because they convey structure much more effectively at that level. Therefore, pseudocode tends to be much more informal and a case of "whatever works". Some people choose to write their pseudocode very much as though it were a true programming language with very formal constructs. In fact, a common project in some software engineering courses is to devise a formal pseudocode and a translator that converts the pseudocode into actual code in some programming language. On the other end of the spectrum, some people write their pseudocode almost like a free-verse description of what the program needs to do.
The authors of your text tend to be more toward the latter end of the spectrum. You will probably notice that they seldom present highly detailed steps and generally prefer to describe what the input is, what the output should be, and then discuss how they go about producing that output. This is perfectly acceptable. You should probably also note that when they do represent an algorithm as a list of steps, they tend to use statements like "Repeat lines 15 through 17 while x < 4". This is also perfectly valid, but I think you will quickly discover a major disadvantage to writing your pseudocode this way. The frequent references to specific line numbers does not present a problem to someone reading the pseudocode, but when you're writing your pseudocode you will find two things to be very true - you will frequently be referring to lines that haven't been written yet meaning that you will have to go back and add the line numbers, once known, to earlier instructions. Worse, you will find that the line numbers keep changing as you add and delete lines. Just adding a single line at the top of your list means that every line number that appears in any instruction now has to be updated.
Fortunately, this last drawback can be avoided in a couple of ways. The first way is to provide labels for some of the instructions - namely the lines referred to in other instructions. The other way is to use indenting or some other means of showing that some instructions are controlled by other, higher level instructions. Your authors use this latter approach in their solution to Exercise 1.5.7 (in the back of the book). If you look at line 14, you will notice that the authors could have left out the statement "repeat lines 15 and 16" because lines 15 and 16 are the only two lines that are indented more than line 14. The same is true every place else the level of indenting changes. But also notice that, relying on the indenting alone, can get confusing. For instance, it's hard to tell exactly which of the instructions line 19 is associated with (and the fact that it is on the next page simply makes matters worse).
Fortunately again, there is a pretty easy way around this as well, though your authors elect not to use it. It is called the "legal outline". In legal documents it is necessary to be able to refer to specific sections or even specific clauses of the document in an unambiguous fashion and a simple means of numbering sections and their component parts was adopted for that purpose. This, combined with a commitment to adhere to the use of structured programming constructs (sequence, selection, and repetition), allows the pseudocode to be written entirely without the need to refer to line numbers within any of the instructions.
But using the legal outline notation has drawbacks as well - most notably, it is cumbersome, especially if you are doing it on paper. You can avoid most of this by using the indenting alone to show the structure and adding in the outline numbers at the end. Or, you could completely forego the outline numbers altogether - but if you do that you must be certain that the indenting structure is very clear. This is reasonably easy to accomplish with a fixed-pitch font but can be difficult to accomplish with a proportional pitch font. Another way to circumvent this - and in fact to use it to your advantage - is to develop your pseudocode with a tool that is set up to work with legal outlines. Fortunately, most reasonably featured word processors, including Word, are capable of doing this. Although you cannot submit a Word document as your pseudocode, you can copy and paste the contents of the Word document to an ASCII text file (using Notepad, for instance) and the numbering will be carried over in the operation, which is very convenient.
To aid in communication - particularly between you and the grader (the value of which should be relatively obvious) it is recommended that the problem be decomposed into a set of hierarchical tasks. The lowest-level tasks should either be tasks that are very straightforward to implement directly in C (using your level of knowledge) or the specific instructions for performing the task should be provided. By beginning each line with one of the keywords discussed below, the chance for miscommunication between you and the grader is greatly diminished.
Documentation keywords describe what needs to be done or provides information about why something is being done. You will quickly discover that, if you have done a decent job of writing your pseudocode, that these lines make very useful comment lines in your final code.
A TASK statement is something that the program must perform but that is described at a level more abstract than what can be coded directly. One way to think of it is that you break a problem down into a set of TASKs. Each TASK can, in turn, be broken down into more narrowly defined TASKs. At some point, the TASK can be described in terms of steps that can be directly implemented. From one perspective, anytime a TASK: keyword is used, it means that there should (or at least could) be a subordinate level of the hierarchy which is the pseudocode for that TASK. In practice, that pseudocode need not be present if the TASK is sufficiently narrow that the person implementing it can go directly from the TASK description to the actual code without the benefit of the detailed steps.
A REM statement is merely a remark or comment. They are useful if the TASK statement proves to be insufficient to convey all the desired information or if the reason that something is done or why it works is not obvious..
Action keywords are the lines that actually do the work. There are three basic actions that can be carried out: changing the value stored at some location in memory, getting input from some device, or generating output to some device. We will use the SET, GET, and PUT keywords for these actions respectively.
This is an "action" keyword that denotes performing some operation that changes a value in memory. The most common example would be the evaluation of some equation.
This is an "action" keyword that denotes an output operation, generally to the screen. If the destination is anything other than the screen, such as a file or the serial port, then that should be explicitly stated.
This is an "action" keyword that denotes in input operation, generally from the keyboard. It is generally understood that there is an implied SET action involved where the value brought in gets stored in some memory location. If the source is anything other than the keyboard, such as a file or the serial port, then that should be explicitly stated.
While the action keywords perform the actual work, they are insufficient in and of themselves to write all but the most trivial programs. Of the three structured programming constructs, the action keywords are only sufficient to implement the first of them, namely a sequence of instructions. A program's true power comes from the other two - selection and repetition - because they give it the ability to select whether a particular action will actually be carried out based on the information made available to it at the time that it is executed. This ability is the result of controlling the flow of the program which is the purpose of the flow control keywords.
Because flow control is a more complex task that merely executing a single statement, all but the simplest flow control keywords are used in groups and there are some options in how to use them depending on the specific situation.
Selection - Case 1
- SEL: (test condition)
- TRUE:
- Statement(s) to be executed if test condition is TRUE
- FALSE
- Statement(s) to be executed if test condition is FALSE
Selection - Case 2
- IF: (test condition)
- Statement(s) to be executed if test condition is TRUE
- ELSE:
- Statement(s) to be executed if test condition is FALSE
The advantage of Case 1 is that it clearly identifies the block as a selection construct, but it is a bit more involved than is usually necessary. The format of Case 2 is very close to the format of the actual C code that would result and is therefore a bit more straightforward to convert in the coding process, but not enough so as to be a significant factor.
In a legal outline, the ELSE: statement in Case 2 would be numbered one more than the IF: statement - in other words, if the IF: statement was numbered 3.4.2.6) then the ELSE: statement would be numbered 3.4.2.7). This can be useful or confusing depending upon how you thing of it. If you think of the test condition controlling a single selection construct, then it would be nice if the controlling expression was one level in the outline and everything it controls was at a lower level. So this could be a bit confusing. However, this format actually emphasizes the fact that, in C, an "else" statement truly is a separate statement and that it must immediately follow an "if" statement that is at the same level of control. Neither convention is significantly better than the other - and you should quickly get comfortable with whichever you choose to use.
Repetition - Case 1
- LOOP:
- WHILE: (test condition)
- Statement(s) to be executed if test condition is TRUE
Repetition - Case 2
- LOOP:
- Statement(s) to be executed if test condition is TRUE
- WHILE: (test condition)
These two cases map directly into the while() and do/while() looping constructs of the C language. In Case 1, the test condition is evaluated prior to making the first pass through the statements controlled by it and, as a result, the possibility exists that those statements won't be executed even once. The only difference in Case 2 is that the statements controlled by the test condition are executed one time and the test is evaluated after that first pass. If the test condition is TRUE then another pass is made - and the test condition evaluated at the end of that and each succeeding pass until the test finally fails.
While the two cases above are more than adequate to represent any looping logic - in fact, either one of them by itself is sufficient, just more cumbersome in some cases - the logic is sometime clearer to the reader if it is expressed in terms of repeating the loop until some some condition is met - meaning that the loop is terminated as soon as the test condition becomes TRUE.
Repetition - Case 3
- LOOP:
- UNTIL: (test condition)
- Statement(s) to be executed if test condition is FALSE
Repetition - Case 4
- LOOP:
- Statement(s) to be executed if test condition is FALSE
- UNTIL: (test condition)
Although C does not support a "loop until" construct (some languages do) converting Case 3 to an equivalent form of Case 1 is trivial - you simply invert the test condition. Similarly, Case 4 can be converted to Case 2 by the same mechanism.
Just as the selection construct can be streamlined, so too can a couple of the repetition constructs.
Repetition - Case 5 (streamlined version of Case 1)
- WHILE: (test condition)
- Statement(s) to be executed if test condition is TRUE
Repetition - Case 6 (streamlined version of Case 3)
- UNTIL: (test condition)
- Statement(s) to be executed if test condition is FALSE
Streamlining the other two is more difficult because, since the test comes at the end of the statement within the loop, it is very useful to mark the beginning of those statements in such a way that the fact that it is a loop is readily apparent to the reader. The LOOP: statement does that about as well as any other option would.
As you code loops, you will discover that it is frequently the case that there are steps that are logically associated with the loop but which must reside outside of the loop code. The most common by far is the need to initialize certain variables, especially counters, prior to entering the loop. Much less frequently, it is necessary to perform some cleanup tasks immediately after the loop is exited. A pseudocode construct that gathers all of these together so that their association is obvious is the following:
Repetition - Case 7
- REP:
- PRE:
- Statement(s) to be executed prior to entering loop
- WHILE: (test condition)
- Statement(s) to be executed if test condition is TRUE
- LOOP:
- POST:
- Statement(s) to be executed prior after the loop is finished
The above can be easily altered so as to cover all four of the first four cases. As shown, it implements Case 1. By switching the WHILE: and LOOP: statements it implements Case 2. Similarly, Case 3 is obtained simply by changing the WHILE: to UNTIL: and swapping the UNTIL: with the LOOP: then generated Case 4.
Flowcharts are a graphical means of representing an algorithm, as should be expected, they have advantages and disadvantages compared to pseudocode. One of their primary advantages is that they permit the structure of a program to be easily visualized - even if all the text were to be removed. The human brain is very good at picking out these patterns and keeping them "in the back of the mind" as a reference frame for viewing the code as it develops.
Most programmers also find it easier to sketch flowcharts on a piece of paper and to modify them by crossing out connection arrows and drawing new ones that they would working with pseudocode by hand. By the same token, most programmers do not like to develop flowcharts in an electronic format because the overhead of creating and modifying it is generally more than they want to deal with while pseudocode lends itself to such electronic development.
Furthermore, if the pseudocode is already in an electronic format that has been structured to lend itself to translation to the final language - such as the one recommended in the previous section - then doing so can be a very simply matter of copying the pseudocode to a new file, overlaying the necessary syntax associated with the language, and compiling the result. This can be a powerful advantage of pseudocode over flowcharts where the entire source code still has to be typed by hand unless you are fortunate to have a tool that can take a flowchart - typically developed using that same tool - and translating it to directly to code. Such tools do exist - and they tend to be rather expensive.
Now that we have looked as some of the pros and cons of flowcharts relative to pseudocode, let's delve into flowcharting itself. The idea behind a flowchart is that it links together a series of blocks each of which perform some specific task. Each of these tasks is represented by a block and has exactly one arrow leading to it and, more importantly, one arrow exiting from it. This is key to the concept of a "structured program".
The shape of the block may convey additional information about what is happening. For instance, a rectangular block is frequently used to indicated that a computation is occurring while a slanted parallelogram is used to indicate some type of input or output operation. The diversity of shapes that can be used and what they mean is staggering - for instance a different shape can be used to indicated output to a tape drive versus to a hard disk or to indicate output in text format verses binary format. By using such highly specialized symbols, much of what is happening can be conveyed by the symbols themselves. But the power of using these distinctions is generally only useful to people that work with flowcharts continuously, professionally, and who are describing very large and complex systems. At our level, it is far better to restrict ourselves to a minimum number of shapes and explicitly indicate any information that otherwise might have been implied by using a different shape.
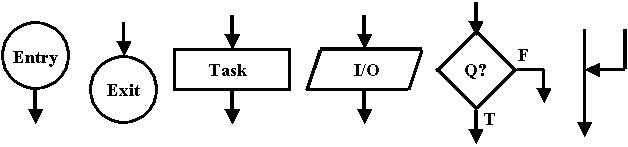
The shapes we will use are the circle, the rectangle, the parallelogram, the diamond, and the arrows that interconnect them.

The circle indicates the entry and exit point for the program - or for the current segment of the program. The entry point has exactly one arrow leaving it and the exit point has exactly one arrow entering it. Execution of the program - or of that segment of the program - always starts at the entry point and finishes at the exit point.
The rectangle represents a task that is to be performed. That task might be as simple as incrementing the value of a single variable or as complex as you can imagine. The key point is that it also has a single entry point and a single exit point.
The parallelogram is used to indicate that some form in input/output operation is occurring. They must also obey the single entry single exit point rule which makes sense given that they are a task-block except with a slightly different shape for the symbol. We could easily eliminate this symbol and use the basic rectangle but the points at which I/O occur within our programs are extremely important and being able to easily and quickly identify them is valuable enough to warrant dealing with a special symbol.
Since a Task block can be arbitrarily complex, it can also contain I/O elements. Whether to use a rectangle or a parallelogram is therefore a judgment call. One way to handle this is to decide whether a task's primary purpose is to perform I/O. Again, that is a judgment call. Another option is to use a symbol that is rectangular on one side and slanted on the other indicating that it is performing both I/O and non-I/O tasks.
The diamond represents a decision point within our program. A question is asked and depending on the resulting answer, different paths are taken. Therefore a diamond has a single entry point but more than one exit point. Usually, there are two exit points - one that is taken if the answer to the question is "true" and another that is taken if the answer to the question is "false". This is sufficient to represent any type of branching logic including both the typical selection statements and the typical repetition statements. However, most languages support some type of "switch" or "case" statement that allows the program to select one from among a potentially large set of possible paths. The basic two-exit-point diamond is fully capable of representing this construct, but it is generally cleaner and more useful to represent it using a as many exit points from the diamond as there are paths.
The arrows simply show which symbol gets executed next. The rule is that once an arrow leaves a symbol, it must lead directly to exactly one other symbol - arrows can never fork and diverge. They can, however, converge and join arrows coming from other blocks.