Exam #2 Review
(Last Mod: 27 November 2010 21:38:37 )
The speed of light (in a vacuum) is exactly 299,792,458 meters/second. How many digits are required to express this in base 3?
The speed of light (in a vacuum) is exactly 299,792,458 meters/second. Express this in base 7.
The speed of light (in a vacuum) is exactly 299,792,458 meters/second. Express this in hexadecimal.
The speed of light (in a vacuum) is exactly 299,792,458 meters/second. Express this as an IEEE 754 single precision floating point value stored at memory location 0x3C08 in Little Endian format.
The value pi (3.14159265) is stored as a four-byte IEEE-574 single precision floating point number in Little Endian format. It is then mistakenly read as a four-byte IEEE-574 single precision floating point number in Big Endian format. What is the base-10 value that would be read as a result?
A particular number is represented using two bytes in signed binary, offset binary, and two's compliment format. In no particular order, the three representations yield values of 0x2020, 0x2020, and 0xA020. What is the original number?
A particular number is represented using two bytes in signed binary, offset binary, and two's compliment format. In no particular order, the three representations yield values of 0xA020, 0x5FE0, and 0xDFE0. What is the original number?
The string, "Time 2 Go!" is stored at memory location 0xC340. Indicate the values (using the actual numbers - in hex) that are stored in each of the relevant memory locations.
The following bytes are stored beginning at memory location 0xC34D: 0x66, 65, 68, 00, 47, 6F, 6F, 64, 00, 73, 6F, 2D, 73, 6F, 00. What string is stored at memory location 0xC351?
Performing all computations directly in hexadecimal, write the result of 0xFADE divided by 0x2BAD in quotient-remainder form (i.e., the quotient is an integer).
Prepare a table that shows the decimal value represented by each of the sixteen possible 4-bit binary patterns under the following representations: Pure binary, signed binary, offset binary (excess 8), one's compliment, and two's compliment.
To take the negative of a number when using the two's compliment format you can use the simple algorithm where you first invert all of the bits and then add one to the result. Starting with the definition of an "additive inverse", show where this algorithm comes from. Don't just regurgitate the algorithm or show an example of how it is used. Derive the algorithm based on the properties of the additive inverse and fixed width binary integers.
Given two two-byte binary bit strings A and B, what is the practical net effect of executing the following three statements:
A = A^B
B = A^B
A = A^B
Note that '^' indicates bitwise XOR. This is a general question regarding the impact of performing three successive XOR operations on the same variables as shown above.
Write a code fragment that asks the user to enter a floating point number and then outputs the square root of that number to the screen. You may use any function from the math library except pow() and sqrt().
Assuming that a prompt has already been issued asking the user to enter a single character and hit enter, use getc() and putc() to write a code fragment that retrieves this character and then outputs the same character except that if the character entered was upper case it outputs the lower case equivalent. You may not use any standard library functions other than getc() and putc().
Assuming that a prompt has already been issued asking the user to enter a single character and hit enter, use getc() and putc() to write a code fragment that retrieves this character and then outputs the same character except that if the character entered was lower case it outputs the upper case equivalent. You may not use any standard library functions other than getc() and putc().
Given two points (x1,y1) and (x2,y2) and a value x, write a code fragment that computes the y corresponding to x assuming a linear relationship between y and x.
Given a strictly positive floating point value x and a floating point value y, write a code fragment that outputs x^y. You may NOT use the pow() function.
Given a positive floating point value x, write a complete function that returns the logarithm of x to the base b (where b is a strictly positive floating point value).
What is the output of the following program:
int main()
{
int i;
for(i=0; i<5; i++);
{
printf("%i\n",i);
}
return(1);
}What are the values of x, y, and z at the end of the execution of the following code fragment:
int main()
{
double x,y,z;
....
x = 2.0;
y = 8.0;
z = x+y/((y>x)?(x):(y));Draw a flowchart for the following while loop
int main()
{
int i;
....
while(i++<42)
{
printf("%i\n",i);
}
....
How should two doubles be compared for equality? Write a code fragment that performs this check without using any functions from the math library.
EXTRA CREDIT
The following is the extra credit problem on the exam. The only potential difference between this problem and the actual exam problem will be the specific number of digits that you are asked about.
For
large values of n, the factorial of n can be closely approximated by the
following equation:
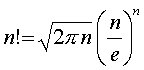
For instance, for n = 10 the above equation, known as the Stirling Formula, yields a value that is within 1% of the correct answer.
(5
pts) Write a complete C function
called fact_digits() that takes a double n as the argument and returns a
floating point (type double) value that is the number of digits in n!. Your
function needs to be able to accept values of n for which n! would be far too
large to accommodate even in a variable of long double. For instance, the user
might wish to use your function to discover what the first value of n! is that
has more than one trillion (1012) digits. A long double, on most compilers,
can't even represent a number with 15,000 digits. Hint: How many digits are in
12345? What is the base ten log of 12345?
(5
pts) Within 1%, what IS the first value of n for which n! has more than a
trillion (1012) digits. Hint: You can do this reasonably quickly on
your calculator - but be sure to be finished with the rest of the exam first.
Show your work for full credit.