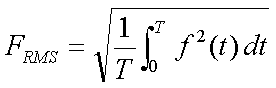
ECE 1011 - Summer 2003
(Last Modified: 04 Nov 2010 )
This is actually a two part homework assignment (as all of the others should have been).
Part I: Write a program to compute the RMS value of a waveform.
This "should" be a straight forward assignment that lets you use some of the concepts we have already explored and without requiring you to use any new programming topics. That will allow us to hold off on the actual implementation of the Maze Game until we have dealt with arrays.
Because this is a change in what you were expecting, you have access to the flowchart for the program so that you can focus on the implementation details and not the logic.
Part II: Perform the Top-Level design of the Maze Game program that will be implemented as Homework #5.
The more effort you put into this part of the assignment, the easier you will find Homework #5. The goal here is to break the overall problem into several manageable pieces, determine how those pieces interact to form an overall solution, and then sketch out how the individual pieces might be solved. Unlike Part I, here I want you to focus on the logic and not the implementation details.
The RMS value - the Root of the Mean of the Square - of a set of data is a frequently used metric to describe at least one property of that data set. In some cases it is a purely arbitrary metric where the value lies in providing a well-defined metric that can be evaluated for different data sets and the results compared with each other. We saw this use of the concept of RMS used in development of Least Squares Linear Regression. In other cases the RMS value has physical meaning. For example, if an arbitrary voltage waveform is applied to a resistor, then some average power level will be delivered to that resistor. The RMS value of that waveform is equal to the DC voltage that would deliver the same power to that same resistor.
For a continuous function f(t), the RMS value of that waveform is given by:
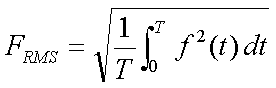
While you have spent a great deal of time in your math classes learning how to perform integration symbolically, you probably first learned what the concept of integration was by performing it numerically. You have also spent a great deal of time setting up integrals, such as would be needed to find the volume of a solid of rotation, by actually setting up the equations that would be needed to perform the integration numerically and then, at the proper point, simply taking the limit as the differential element goes to zero and thereby turning the finite summation expression into an integral expression. Hence, performing the integration numerically should not be a significant hurdle.
Recall that to integrate a function numerically, you define a differential slice (dt) and multiply it by the value of the integrand at the current value of t. This yields an incremental area between that value of t and t+dt that is an approximation of the true incremental area. You then add up all of the incremental areas that lie between the limits of integration to get the result of the integral.
Looking at the above expression for FRMS, you can see that this is only part of the answer - namely the "Squares" part of RMS. But it is the most difficult part and to get the final answer all you have to do is then find the "Mean" by dividing by the span of integration and finally you must obtain the "Root" by taking the square root of the mean.
The assignment:
Write a program that computes and reports the RMS value of an arbitrary waveform between two limits supplied by the user. If the user fails to supply the two values in ascending order, you should reverse them. If the two limits are equal, then you should issue an error message and terminate your program. You should also ask for the number of time increments to use and, if the user enters any value that is not strictly greater than zero, use the default number of time steps given by the constant TIMESTEPS defined in waveform.h should be used instead.
Your arbitrary waveform will come from a function with the following prototype:
double waveform(double t);
This prototype will be in a file called waveform.h (stored in the same directory as your source code) that you access by using
#include "waveform.h"
Normally, the actual function would be defined in a separate source code file (probably called waveform.c) that would be compiled separately and then linked to your program after it is compiled. To keep things simple, we are going to cheat and merely place the definition of waveform() in the .h file. Your program won't know the difference.
As far as your program is concerned, you have a function named waveform() that, if you pass it a value of time t, will return the value of the waveform at that time. Just like the sin() function will or any of the math library functions would.
For testing purposes, you might start out with the following definition of waveform() in the waveform.h file:
#define TIMESTEPS (100000L)
double waveform(double t);
// The following would normally not be in the *.h file
#include <math.h>
double waveform(double t)
{
double y;
y = sin(t); // Replace this with any code you like.
return(y);
}
You can modify the definition of the waveform() function as much as you like to test your code. The RMS value of a sine wave (over an integral number of half periods) is sqrt(2)/2 or 0.707.
When you submit your source code, just submit your *.c file. I will have my own waveform.h file that has a particular waveform() function that will be used to evaluate your code.
After reading the description of the Maze Game, perform the following tasks:
A Top Level Decomposition Outline of the Maze Game that identifies the major blocks that perform relatively self-contained high level tasks might look like the following:
Continue with the decomposition of the Maze Game for several more levels. The goal is to break it down to sufficiently small problems that you can tackle each problem with confidence. You should notice that, at some point, your Decomposition Outline starts becoming pseudocode (generally indicated by the appearance of selection and looping structures in the descriptions).
Continue breaking down the problem by outlining the upper levels in terms of fairly low level tasks. For instance, a portion of the decomposition outline for a fairly major segment of the game might have been described as:
You might now write pseudocode for these two blocks along the lines of:
action = GetAction();
if(action is turn left)
then (turn the mouse to the left);
if(action is turn right)
then (turn turn the mouse to the right);
if(action is go forward)
then if(square ahead is open)
then (move the mouse forward)
Now catalog the lower level tasks that you will need to be able to perform to implement the game. These are the functions and/or code blocks that you will need to write as part of the next homework assignment. Examples of these might include: